
21.解:(I)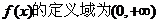
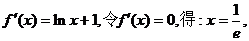 ………………1分
………………1分
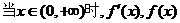 的变化的情况如下:
的变化的情况如下:
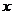 |
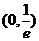 |
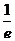 |
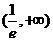 |
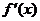 |
- |
0 |
+ |
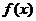 |
 |
极小值 |
 |
………………3分
所以, ………………4分
………………4分
(II)当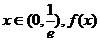 单调递减且
单调递减且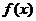 的取值范围是
的取值范围是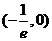 ;
;
当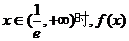 单调递增且
单调递增且
下面讨论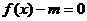 的解;
的解;
所以,当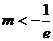 时,原方程无解; ………………6分
时,原方程无解; ………………6分
当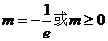 时,原方程有唯一解;
时,原方程有唯一解;
当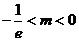 时,原方程有两解 ………………8分
时,原方程有两解 ………………8分
(III)原不等式可化为:
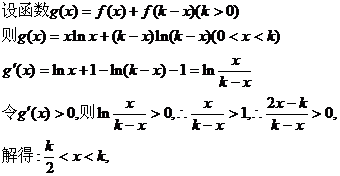
令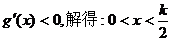 ………………10分
………………10分
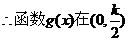 上单调递减,在
上单调递减,在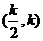 上单调递增,
上单调递增,
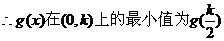 ………………12分
………………12分
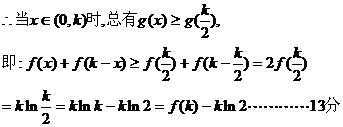
令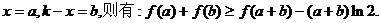 …………14分
…………14分
(1)证明:∵AD是两圆的公切线,
∴AD2=DE×DG,AD2=DF×DH,
∴DE×DG= DF×DH, ∴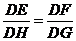 ,
,
又∵∠EDF=∠HDG,∴△DEF∽△DHG。………………………4分
(2)连结O1 A,O2A,∵AD是两圆的公切线,
∴O1A⊥AD,O2A⊥AD,
∴O1O2共线,
∵AD和BC是⊙O1和⊙O2公切线,DG平分∠ADB, DH平分∠ADC,
∴DG⊥DH,∴AD2= O1A×O2A,………………………8分
设⊙O1和⊙O2的半径分别为9x和16x,则AD=12x,
∵AD2=DE×DG,AD2=DF×DH,
∴144x2=DE(DE+18x),144x2=DF(DF+32x)
∴DE=6x,DF=4x,∴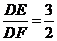 。………………………10分
。………………………10分
选修4-4:坐标系与参数方程:
20.解:(Ⅰ)由题意知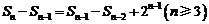 即
即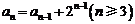
∴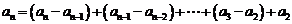
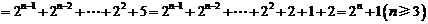
检验知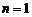 、
、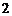 时,结论也成立,故
时,结论也成立,故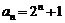 .
.
(Ⅱ)
由于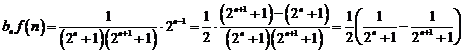
故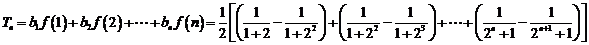
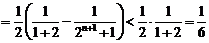 .
.
19.(I)将抛物线方程配方得 ,
,
设抛物线的顶点为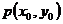 , 则
, 则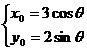 , 消去
, 消去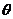 得
得 .
.
故抛物线C的顶点P的轨迹E的方程: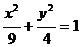 . ………………5分
. ………………5分
(Ⅱ)由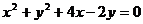 得圆心M(-2,1),
得圆心M(-2,1),
∵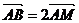 ∴M是AB的中点,
易得直线
∴M是AB的中点,
易得直线 不垂直x 轴,
不垂直x 轴,
可设 的方程为
的方程为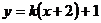 ,代入轨迹E的方程得:
,代入轨迹E的方程得:
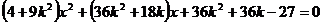 ,
,
设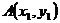 ,
,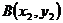 , 则
, 则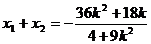 ,
,
∵M是AB的中点, ∴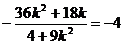 , 解得k=
, 解得k=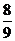 .
.
∴直线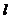 的方程为
的方程为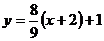 , 即
, 即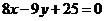 ………12分
………12分
18.(1)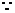 P
P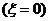 =
= P
P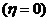 =
=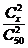
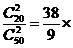
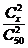
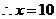
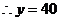
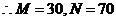
(2)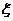 取值为0,1,2
取值为0,1,2
P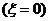 =
= =
=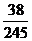 , P
, P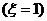 =
=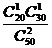 =
=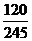 ,P
,P =
=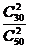 =
=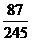 ,
,
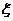 |
0 |
1 |
2 |
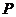 |
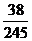 |
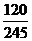 |
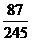 |
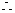
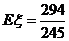 -----7分
-----7分
P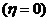 =
=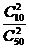 =
=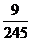 P
P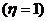 =
=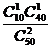 =
=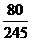 P
P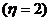 =
=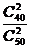 =
=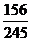
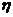 |
0 |
1 |
2 |
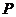 |
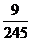 |
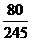 |
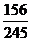 |
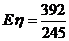 ------9分
------9分
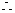
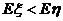 说明药物有效
----10分
说明药物有效
----10分
(3)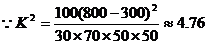 ---------11分
---------11分
由参考数据知不能够以97.5%的把握认为药物有效。 ------12分
13.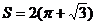 14.
14.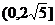 15.
15.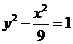 16. PF1·PF2=PC·PD.
16. PF1·PF2=PC·PD.
17.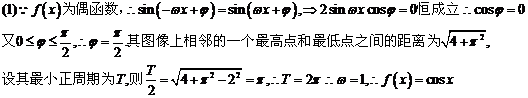
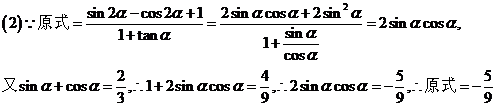
24.(本小题满分10分)
设函数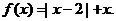
(1)求函数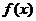 的值域;
的值域;
(2)若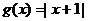 ,求
,求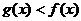 成立时
成立时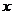 的取值范围。
的取值范围。
BCAD AAAD AADA
23.(本小题满分10分)
已知圆锥曲线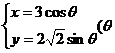 是参数)和定点
是参数)和定点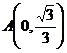 ,F1、F2是圆锥曲线的左、右焦点。
,F1、F2是圆锥曲线的左、右焦点。
(1)求经过点F2且垂直地于直线AF1的直线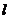 的参数方程;
的参数方程;
(2)以坐标原点为极点,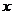 轴的正半轴为极轴建立极坐标系,求直线AF2的极坐标方程。
轴的正半轴为极轴建立极坐标系,求直线AF2的极坐标方程。
选修4-5:不等式选讲:
22.(本小题满分10分)
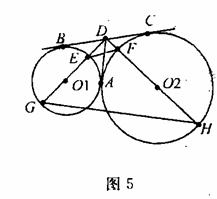 如图5,⊙O1和⊙O2 公切线AD和BC相交于点D,A、B、C为切点,直线DO1与⊙O1与E、G两点,直线DO2交⊙O2与F、H两点。
如图5,⊙O1和⊙O2 公切线AD和BC相交于点D,A、B、C为切点,直线DO1与⊙O1与E、G两点,直线DO2交⊙O2与F、H两点。
(1)求证: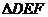 -
-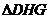 ;
;
(2)若⊙O1和⊙O2的半径之比为9:16,求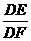 的值。
的值。
选修4-4:坐标系与参数方程:
21.已知函数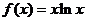
(I)求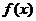 的最小值;
的最小值;
(II)讨论关于x的方程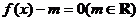 的解的个数;
的解的个数;
(III)当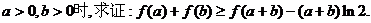
请考生在题22,23,24中任选一题作答,如果多做,则按所做的第一题计分。做题时用2B铅笔在答题卡上把所选题目对应的题号涂黑。
选修4-1:几何证明选讲:
20.已知数列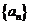 中,
中,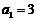 ,
,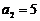 ,其前
,其前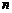 项和
项和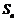 满足
满足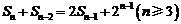 .令
.令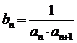 .
.
(Ⅰ)求数列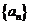 的通项公式;
的通项公式;
(Ⅱ)若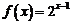 ,求证:
,求证: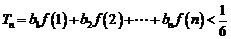 (
(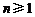 )。
)。
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com