22．(本小题满分14分)已知f(x)是定义在(－∞，+∞)上的偶函数，且满足

f(x+2)＝f(x)，当[2，3]时，f(x)＝－2(x－3)²+4.

　　　　 (1)当[0，2]时，求f(x)的解析式；

　　　　 (2)若矩形ABCD的两个顶点A、B在x轴上，C、D在函数y＝f(x)(0≤x≤2)的图象上，求矩形ABCD面积的最大值.

安谷中学2010届高三第二次模拟考试

21.(本小题满分12分)

随着我国加入WTO，某企业决定从甲、乙两种畅销产品中选择一种进行投资生产，打入国际市场.已知投资生产这两种产品的有关数据如下表(单位：万美元)

项目 　 类别	年固定成本	每件产品成本	每件产品 销售价	每年最多生产的件数
甲产品	30	a	10	200
乙产品	50	8	18	120

其中年固定成本与生产的件数无关，a为常数，且4≤a≤8.另外，年销售x件乙产品时需上交0.05x²万美元的特别关税.

(1)写出该厂分别投资生产甲、乙两种产品的年利润与生产相应产品的件数

x(x∈N)之间的函数关系式；

(2)分别求出投资生产这两种产品的最大年利润；

(3)如何决定投资可获最大年利润？

20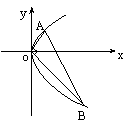．(本小题满分12分)已知Rt△OAB的三顶点O、A、B都在抛物线C：y²＝2px(p>0)上(如图)，OA⊥OB.

　　　 (1)若直线OA的斜率为2，|AB|＝，求抛物线C

的方程；

　　　 (2)若，求证：与均为定值.

19．(本小题满分12分)在等差数列中，首项，数列满足，

　　　 且.

(1)求数列的通项公式；

(2)求证：.

18．(本小题满分12分)如图所示的一个几何体中，底面ABCD是矩形，AB＝9，BC＝8，EF∥平面ABCD，且EF＝3，EA＝ED＝FB＝FC＝13.

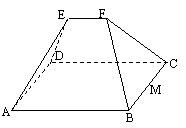　　　 (1)求异面直线AE与CF所成的角；

　　　 (2)求二面角F―BC―D的大小；

17．(本小题满分12分)已知复数，A、B、C是△ABC的内角.

　　　 (1)求A；　 (2)求sinB+sinC的取值范围

16． 已知直线m⊥平面α，直线n平面β，给出下列命题：

　　　 ①α∥βm⊥n；②α⊥βm∥n；③m∥nα⊥β；④m⊥nα∥β.

　　　 其中正确命题的序号是　　　　　　　　 .(要求：把正确命题的序号都填上)

15．我国于2003年10月15日成功发射载人“神舟五号”宇宙飞船，杨利伟随飞船绕地球飞行了14圈，飞船飞行的轨道是以地球的中心为一个焦点的椭圆，近地点距地面200千米，远地点距地面350千米，若地球半径为6371千米，则此椭圆的离心率为　　　 .