读某省人口出生率、死亡率变化图(左图)和人口年龄结构变化图(右图)，回答8-9题。

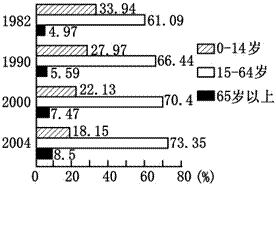
8．2004年该省人口增长的特点是

A．总量呈下降态势　　　　　　　　 B．总量仍呈增长态势

C．总量呈零增长态势　　　　　　　 D．增长模式没有变化

9．按联合国标准，如一地区≥60岁人口占总人口比例达10%或≥65岁的人口达7%，则可视为进入老龄化社会。该省进入老龄化社会的时间约在

A．1990年以前　　　　　 B．1990-2000年之间

C．2000-2004年之间　　　 　D．2004年以后

7．为缓解人口压力，我国应采取的人口增长模式是下图中的

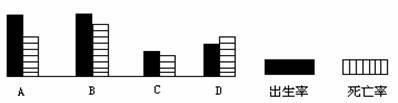
6.目前大多数发达国家的人口增长模式是

A.高出生率、高死亡率、低自然增长率　　　 B.低出生率、高死亡率、高自然增长率

C.高出生率、低死亡率、高自然增长率　　　 D.低出生率、低死亡率、低自然增长率

5.人口增长模式的变化是从

A.出生率的增长开始的　　　　 B.死亡率的下降开始的

C.自然增长率的下降开始　　　 D.生育率的增长开始的

4．下列说法正确的是(　　 )

　 A．自然环境对人口出生率和死亡率的影响都很大

　 B．一个地区的环境人口容量，是由该地区的资源状况所决定的

　 C．环境人口容量就是指一个国家或一个地区的最适合人口

　 D．科技越发达，地球所能容纳的人口数则越少

2005年元月6日，是我国大陆“13亿人口日”，巨大的人口数量，再一次向我们敲响了警钟。同时有关专家还指出，我国近期人口特征表现为三大高峰相汇，即增长高峰、老龄化高峰和就业高峰同时出现。据此回答1-3题。

1．我国人口“增长高峰”的形成主要由于(　　 )

　 A. 人口基数大　 B．人口自然增长率高　 C．人口死亡率低　 D．国外人口迁入

2．我国人口老龄化现象的出现，主要原因是我国　 (　　 )

　 A．养老保险制度较为完善　　　　　　　　 B．严格实行计划生育政策

　 C．人口出现高速增长的态势　　　　　　　 D．人口再生产处于“现代型”阶段

3．从人口普查资料可以看出，我国某些大城市人口死亡率高于农村，其主要原因(　　 )

　 A．农村医疗卫生水平得到改善　　　　　　 B．城市环境问题较为严重

　 C．农村人口的身体素质更好　　　　　　　 D．城市人口老龄化现象更突出

20、(13分)已知椭圆经过点，过右焦点F且不与x轴重合的动直线L交椭圆于两点，当动直线L的斜率为2时，坐标原点O到L的距离为．

(Ⅰ) 求椭圆的方程；

(Ⅱ) 过F的另一直线交椭圆于两点，且，当四边形的面积S=时，求直线L的方程．

17．(本小题满分14分) 已知椭圆的离心率为，椭圆C上任意一点到椭圆两个焦点的距离之和为6。

　 (I)求椭圆C的方程；

　 (II)设直线与椭圆C交于A、B两点，点P(0，1)，且|PA|=|PB|，求直线的方程。

18 (本题满分13分)已知椭圆的左右焦点分别为，．在椭圆中有一内接三角形，其顶点的坐标，所在直线的斜率为．

(Ⅰ)求椭圆的方程；

(Ⅱ)当的面积最大时，求直线的方程．

19 (本小题共14分)

已知椭圆的中心在原点，焦点在轴上，经过点且离心率．过定点的直线与椭圆相交于_，两点．

(Ⅰ)求椭圆的方程；

(Ⅱ)在轴上是否存在点，使为常数？若存在，求出点的坐标；若不存

　　　 在，请说明理由.

16．(本小题满分13分)已知椭圆的短轴长为，且与抛物线有共同的焦点，椭圆的左顶点为A，右顶点为，点是椭圆上位于轴上方的动点，直线，与直线分别交于两点．

　 (I)求椭圆的方程；

　 (Ⅱ)求线段的长度的最小值；

(Ⅲ)在线段的长度取得最小值时，椭圆上是否存在一点，使得的面积为，若存在求出点的坐标，若不存在，说明理由．

15.(本小题共14分)

已知椭圆的焦点是,,点在椭圆上且满足.

(Ⅰ)求椭圆的标准方程；

(Ⅱ)设直线与椭圆的交点为，.

(i)求使 的面积为的点的个数；

(ii)设为椭圆上任一点，为坐标原点，，求的值.