21. (14分)已知数列的前项和为，对一切正整数，点都在函数的图像上，且过点的切线的斜率为．

　 (1)求数列的通项公式．

　 (2)若，求数列的前项和．

　 (3)设，等差数列的任一项，其中是中的最小数，，求的通项公式.

20. (14分)椭圆C的中心为坐标原点O，焦点在y轴上，离心率e = ，椭圆上的点到焦点的最短距离为1-e, 直线l与y轴交于点P(0，m)，与椭圆C交于相异两点A、B，且．

(1)求椭圆方程；

(2)若，求m的取值范围．

19.(14分).设R，函数

(Ⅰ) 当a=2时，试确定函数的单调区间；

　 (Ⅱ) 若对任何R，且，都有，求a的取值范围.

18. (13分)甲、乙两队参加奥运知识竞赛，每队3人，每人回答一个问题，答对者为本队赢得一分，答错得零分.假设甲队中每人答对的概率均为，乙队中3人答对的概率分别为且各人回答正确与否相互之间没有影响.用表示甲队的总得分.　　　

(1)求随机变量的概率分布和数学期望；

(2)用A表示“甲、乙两个队总得分之和等于3”这一事件，用B表示“甲队总得分大于乙队总得分”这一事件，求P(AB).

17.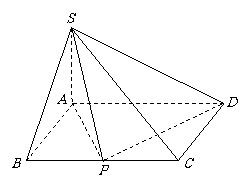(13分)如图，四棱锥的底面是矩形，

底面，为边的中点，与

平面所成的角为，且，.

(Ⅰ)求证：平面；

(Ⅱ)求点到平面的距离；

(Ⅲ)求二面角的大小.

16.(12分)设函数(其中)。且的图像在轴右侧的第一个最高点的横坐标是．

(Ⅰ)求的值；

(Ⅱ)如果在区间上的最小值为，求的值．

15．(几何证明选讲选做题) 如图，⊙的直径的延长线

与弦的延长线相交于点，为⊙上一点，弧

，交于，且，则

_______

14．(坐标系与参数方程选做题)曲线：(为参数)，若以点为极点，轴正半

轴为极轴建立极坐标系，则该曲线的极坐标方程是　　　　　　　 ．

13． 设，集合A={(x，y)|}，B={(x，y)|}．若点P(x，y)∈A是点P(x，y)∈B的必要不充分条件，则的取值范围是　　　　　　 ．

12．为了了解某地区高三学生的身体发育情况，抽查了

该地区100名年龄为17.5岁－18岁的男生体重(kg) ,　

得到频率分布直方图如右.根据上图可得这100名学

生中体重在(56.5,64.5)的学生人数是　　　 　.