18．(本小题满分12分)

解法1：(Ⅰ)过，且，则为异面直线与所成的角．．……3分

(Ⅱ)为的中点。

∵为的中点,∴平面，从而。……5分

∵，……6分

∴平面．………7分

(Ⅲ)由平面，得．

又由(2)平面，∴由三垂线定理得，，∴是二面角的平面角．…………10分

∵，∴．即二面角的余弦值为．…………12分

解法2：以为坐标原点，所在直线分别为轴建立直角坐标系．…2分

　　　 (Ⅰ)∵，，∴．……3分

(Ⅱ)设，∵，，．……

……6分

由平面得，∴∴，即为的中点．

…………7分

(Ⅲ)由(2)知，为平面的一个法向量．

设为平面的一个法向量，则，．

由令．∴．……10分

∴，即二面角的余弦值为．…………12分

17．(本小题满分12分)

解：记选手甲第一、二、三次射击命中目标分别为事件、、，三次均为击中目标为事件，则．

设选手甲在m处击中目标的概率为，则．由m时，得，∴，．∴

．…………4分

(Ⅰ)由于各次射击都是相互独立的，所以选手甲在三次射击中击中目标的概率为

．…………7分

(Ⅱ)由题设知，的可取值为．

，，，．

∴的分布列为

	0	1	2	3

数学期望为．…………12分

16．(本小题满分10分)

解：(Ⅰ)取AB、AC的中点E、F，则

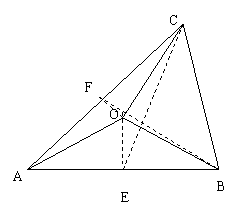
………3分

同理；

所以。………5分

(Ⅱ)

……10分

11．；12．；13．；14．；15．。

1．；2．；3．；4．；5．；6．；7．；8．；9．；10．

1．；2．；3．；4．；5．；6．；7．；8．；9．；10．

21．(本小题满分14分) (注意：在试题卷上作答无效)

已知定义在实数集上的函数，，其导函数记为，且满足：

，为常数．

(Ⅰ)试求的值；

(Ⅱ)设函数与的乘积为函数，求的极大值与极小值；

(Ⅲ)试讨论关于的方程在区间上的实数根的个数．

华中师大一附中高三2010年五月适应性考试

数学试题(理工农医类)答案

(试卷类型：A)

20．(本小题满分14分)(注意：在试题卷上作答无效)

对于函数，若存在使得则称为函数的一个不动点．比如函数有唯一不动点现已知函数有且仅有两个不动点0和2．

(Ⅰ)试求与的关系式；

(Ⅱ)若，各项不为0的数列满足其中为的前项和，试求的通项公式；

(Ⅲ)设记试比较A,B,C的大小，并说明理由．

19．(本小题满分13分)(注意：在试题卷上作答无效)

以为焦点的椭圆过点(，1)．

(Ⅰ)求椭圆的方程；

(Ⅱ)过点(，0)的动直线交椭圆于、两点，试问：在坐标平面上是否存在一个定点，使得无论如何转动，以为直径的圆恒过点? 若存在，求出点的坐标；若不存在，请说明理由．

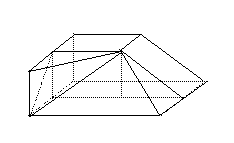
18．(本小题满分12分)(注意：在试题卷上作答无效)

如图，在多面体中，上、下两个底面和互相平行，且都是正方形，底面，．

(Ⅰ)求异面直线与所成的角的余弦值；

(Ⅱ)试在平面内确定一个点，使得平面；

(Ⅲ)在(Ⅱ)条件下，求二面角的余弦值．