6．2000年与1950年相比　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　　 )

　　　 A．欧洲因人口增长较快，所以人均耕地面积减少

　　　 B．大洋洲因人口负增长，所以人均耕地面积增加

　　　 C．北美洲垦殖指数的增长率低于世界平均水平

　　　 D．非洲因机械化水平高，导致垦殖指数上升

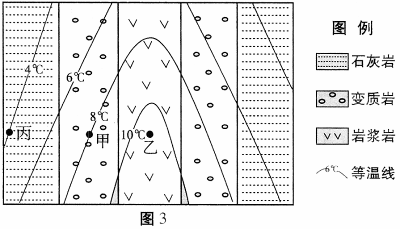　 图3是我国东部某地区岩石与1月均温等值线分布图，读图，回答7-9题。

5．亚洲的垦殖指数较高，可能的原因是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　　 )

　　　 A．地形多种多样，以平原为主

　　　 B．季风气候显著，气象灾害较少

　　　 C．地域辽阔，矿产资源丰富

　　　 D．农垦历史悠久，人口数量最多

4．“土地利用信息数据库”在数字城市规划中不能用于　　　　　　　　　　　　　　　　　　　　　 (　　 )

　　　 A．分析应急避难场所数量　　　　　　　　　　　 B．确定市区停车场的规模

　　　 C．决策公交线路合理布局　　　　　　　　　　　 D．统计城市流动人口数量

垦殖指数是指一地区耕地面积占土地总面积的比例，它是衡量一个地区土地资源开发利用程度的重要指标，通常以百分数表示。表1为世界及各地区耕地垦殖指数和人均占有耕地面积变化表。据表，回答5、6题。

表1

项目 地区	垦殖指数(%)	人均占有耕地面积(公顷/人)
1950年	2000年	1950年	2000年
亚洲	14.7	17.5	0.31	0.14
欧洲	31.3	28.8	0.38	0.27
北美洲	12.0	12.4	1.31	0.81
非洲	5.8	6.3	0.87	0.27
大洋洲	2.0	6.0	1.31	1.84
世界	9.7	11.0	0.51	0.26

3．这一过程中，依次使用的技术是(　　 )

　　　 A．GPS-RS-GIS

　　　 B．RS-GPS-GIS

　　　 C．GIS-RS-GPS

　　　 D．RS-GIS-GPS

2．图中5-6月日照时数变化的原因可能是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　　 )

　　　 A．昼变长夜变短　　　　　　　　　　　　　　　　　　 B．降水量的增多

　　　 C．沙尘暴次数少　　　　　　　　　　　　　　　　　　 D．海拔高度影响

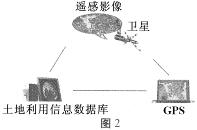　 在未来的农业生产中，依托于地理信息技术，农民首先可定期获得农田长势的影像资料，再经过系统分析，最后把杀虫剂、化肥施用到最需要的农田，从而减少污染、提高产量。依据图文资料，回答3、4题。

1．北京市2008年降水量与多年平均值相比　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　　 )

　　　 A．4、5月降水偏多，有效缓解旱情　　　　 B．7月降水少，因受低气压控制

　　　 C．9月降水多，有利于春小麦的播种　　　 D．全年降水量少，属于偏旱年份

2010．05

本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分，共300分。考试时间150分钟。考试生务必将答案答在答题卡上，在试卷上作条无效。考试结束后，将本试卷和答题卡一并交回。

第Ⅰ卷(选择题，共140分)

本卷共35小时，每小题4分，共计140分。在每小题列出的四个选项中，选出最符合题目要求的一项。

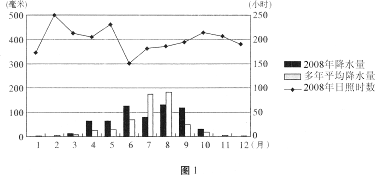　 图1为北京市降水量与日照射数统计图，其中日照时数主要与昼夜长短、天气状况、海拔高度等因素有关。读图，回答1、2题。

21．(本小题满分14分)

　解：(Ⅰ)，则，，又，

　　　 …………2分

(Ⅱ)令，则

，…3分

令，得，且，

当为正偶数时，随的变化，与的变化如下：

		0		0
				极大值		极小值

所以当时，_极大=；当时，_极小=0．…………7分

当为正奇数时，随的变化，与的变化如下：

		0		0
				极大值

所以当时，_极大=；无极小值．…………10分

(Ⅲ)由(Ⅰ)知，，即，

所以方程为，…………11分

，…………12分

又，而对于，有(利用二项式定理可证)，

。…………13分　

综上，对于任意给定的正整数，方程只有唯一实根，且总在区间内，所以原方程在区间上有唯一实根．…………14分

20．(本小题满分14分)

解：(Ⅰ)由得，。由题设知为该方程的两个根。

(Ⅱ)若c=2,则b=2.

…①，又由………②

②式-①式可得：

当=1时，有

……………6分

故

(Ⅲ)

以下首先证明不等式

事实上要证

则

　　　 另一方面我们又设函数，则

。

故在上单调递减，

我们取

综上：

分别令=1，2，3，…，2009得：

将这2009个式子累加得：

19．(本小题满分13分)

解法一： (Ⅰ)设椭圆方程为，由已知。

又．

所以，椭圆C的方程是+ =1．…………4分

　　 (Ⅱ)若直线l与x轴重合，则以AB为直径的圆是x²+y²=1, …………5分

若直线l垂直于x轴，则以AB为直径的圆是(x+)²+y²=．…………6分

由解得即两圆相切于点(1，0)．…………7分

因此所求的点T如果存在，只能是(1，0)．

事实上，点T(1，0)就是所求的点．证明如下：

当直线l垂直于x轴时，以AB为直径的圆过点T(1，0)．

若直线l不垂直于x轴，可设直线l：y=k(x+)．

由即(k²+2)x²+k²x+k²-2=0．………………9分

记点A(x₁,y₁),B(x₂,y₂),则………………10分

又因为=(x₁-1, y₁), =(x₂-1, y₂),

·=(x₁-1)(x₂-1)+y₁y₂=(x₁-1)(x₂-1)+k²(x₁+)(x₂+)

=(k²+1)x₁x₂+(k²-1)(x₁+x₂)+k²+1

=(k²+1) +(k²-1) + +1=0，

所以TA⊥TB，即以AB为直径的圆恒过点T(1，0)．

所以在坐标平面上存在一个定点T(1，0)满足条件．…………13分

解法二：(Ⅰ)由已知，设椭圆C的方程是．

因为点P在椭圆C上，所以,解得，

所以椭圆C的方程是：．………………4分

(Ⅱ)假设存在定点T(u，v)满足条件．

同解法一得(k²+2)x²+k²x+k²-2=0．………………6分

记点A(x₁,y₁)，B(x₂,y₂),则…………7分

又因为=(x₁-u, y₁-v), =(x₂-u, y₂-v),及y₁=k(x₁+),y₂=k(x₂+)．

所以·=(x₁-u)(x₂-u)+(y₁-v)(y₂-v)

=(k²+1)x₁x₂+(k²-u-kv)(x₁+x₂)+k²-v+u²+v²

=(k²+1) +(k²-u-kv)·+ -v + u²+v²，

=．…………10分

当且仅当·=0恒成立时，以AB为直径的圆恒过点T．

·=0恒成立等价于解得u=1,v=0．此时，以AB为直径的圆恒过定点T(1，0)．……………………13分

当直线l垂直于x轴时，以AB为直径的圆亦过点T(1，0)．

　所以在坐标平面上存在一个定点T(1，O)满足条件．…………13分

解法三：(Ⅰ)同解法一或解法二．………………4分

　　 　(Ⅱ)设坐标平面上存在一个定点T满足条件，根据直线过x轴上的定点S及椭圆的对称性，所求的点T如果存在，只能在x轴上，设T(t，O)．……5分

同解法一得………………7分

又因为=(x₁-t, y₁), =(x₂-t, y₂),所以

·=(x₁-t)(x₂-t)+y₁y₂=(x₁-t)(x₂-t)+k²(x₁+)(x₂+)

=(k²+1)x₁x₂+(k²-t)(x₁+x₂)+k²+t ²

=(k²+1) +(k²-t)++t²

= ．…………………………10分

当且仅当·=O恒成立时，以AB为直径的圆恒过点T．

·=O恒成立等价于解得t=1．

所以当t=1时,以AB为直径的圆恒过点T．……………………12分

当直线l垂直于x轴时，以AB为直径的圆亦过点T(1，O)．

所以在坐标平面上存在一个定点T(1，O)满足条件．………………13分