
3、下列各句中,加点的成语使用不恰当的一项是( )
A.新来的王老师为人不苟言笑,同事们一般都不跟他嘻嘻哈哈,只有谭校长有时还会跟他开点无伤大雅的玩笑。
 美国博物馆的收费可谓各尽所能:有的一部分收费,有的分时段收费,还有的是否交费、交费多少由参观者自行决定。
美国博物馆的收费可谓各尽所能:有的一部分收费,有的分时段收费,还有的是否交费、交费多少由参观者自行决定。
C.一些老师担心,如果学生满足于网上搜索素材,很容易使写作流于复制拼贴,这并非杞人忧天。
D.中、日、韩三国参加这次围棋比赛的运动员,水平都在伯仲之间,谁能胜出,就要看谁具有更好的竞技状态和心理素质了。
2.下列词语解释中,有误的一项是( )
A. 暴霜露 (冒着) 善刀而藏之 (擦拭)
B. 云鬓半偏新睡觉 (睡着) 军壁垓下 (驻军)
C. 与过宋将军 (拜访) 不省所怙(所依靠的人)
D. 哀之而不鉴之(为之悲哀) 貌甚寝 (丑陋)
1.下面词语中加点的字,读音全都正确的一项是( )
A. 绰约 (chuò) 渌水(lù) 邠州(bīn) 踯躅 (chí chú)
B. 玉簟 (diàn) 水汀(tīng) 潋滟 (liàn yàn) 桎梏(zhì kù)
C. 肯綮 (xìng) 訇然 (hōng) 硎石 (xǐng) 刈旗 (yì)
D. 锱铢 (zī zhū) 迤逦 (yǐlǐ) 仇雠 (chóu) 反间计 (jiàn)
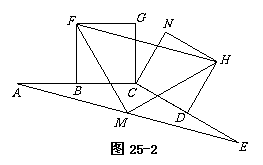
25. 在图25-1至图25-3中,点B是线段AC的中点,点D是线段CE的中点.四边形BCGF和
CDHN都是正方形.AE的中点是M.
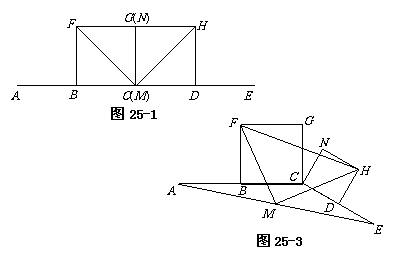
(1)如图25-1,点E在AC的延长线上,点N与点G重合时,点M与点C重合,
求证:FM = MH,FM⊥MH;
(2)将图25-1中的CE绕点C顺时针旋转一个锐角,得到图25-2,
求证:△FMH是等腰直角三角形;
(3)将图25-2中的CE缩短到图25-3的情况,△FMH还是等腰直角三角形吗?
 (不必说明理由)
(不必说明理由)
恭喜你,已经做完所有的题目,请再仔细地检查,可不要留遗憾噢!
24.
如图,已知抛物线C1: 的顶点为P,与x轴相交于A、B两点(点A在
的顶点为P,与x轴相交于A、B两点(点A在
点B的左边),点B的横坐标是1.
(1)求P点坐标及a的值;
(2)如图(1),抛物线C2与抛物线C1关于x轴对称,将抛物线C2向右平移,平移后的抛
物线记为C3,C3的顶点为M,当点P、M关于点B成中心对称时,求C3的解析式;
(3)如图(2),点Q是x轴正半轴上一点,将抛物线C1绕点Q旋转180°后得到抛物线
C4.抛物线C4的顶点为N,与x轴相交于E、F两点(点E在点F的左边),当以点P、N、F为顶点的三角形是直角三角形时,求点Q的坐标.


23.已知: 关于 的一元二次方程
的一元二次方程 ①.
①.
(1)求证: 方程①有两个实数根;
(2)求证: 方程①有两个实数根;
(3)设方程①的另一个根为 ,若
,若 ,
, 为正整数且方程①有两个不相等的整数根时,确定关于
为正整数且方程①有两个不相等的整数根时,确定关于 的二次函数
的二次函数 的解析式;
的解析式;
(4)在(3)的条件下,把Rt△ABC放在坐标系内,其中∠CAB = 90°,点A、B的坐标分别为(1,0)、(4,0),BC = 5, 将△ABC沿x轴向右平移,当点C落在抛物线上时,求△ABC平移的距离。
22.几何模型:
条件:如下左图, 、
、 是直线
是直线 同旁的两个定点.问题:在直线
同旁的两个定点.问题:在直线 上确定一点
上确定一点 ,使
,使 的值最小.
的值最小.
方法:作点 关于直线
关于直线 的对称点
的对称点 ,连结
,连结 交
交 于点
于点 ,则
,则 的值最小(不必证明).
的值最小(不必证明).
模型应用:
(1) 如图1,正方形 的边长为2,
的边长为2, 为
为 的中点,
的中点, 是
是 上一动点.连结
上一动点.连结 ,由正方形对称性可知,
,由正方形对称性可知, 与
与 关于直线
关于直线 对称.连结
对称.连结 交
交 于
于 ,则
,则 的最小值是___________;
的最小值是___________;
(2) 如图2, 的半径为2,点
的半径为2,点 在
在 上,
上, ,
, ,
, 是
是 上一动点,则
上一动点,则 的最小值是___________;
的最小值是___________;
(3)如图3, ,
, 是
是 内一点,
内一点, ,
, 分别是
分别是 上
上
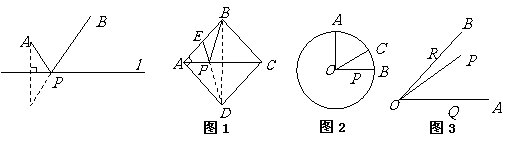 的动点,则
的动点,则 周长的最小值是___________.
周长的最小值是___________.
21. 为了了解延庆的旅游情况,小明收集了延庆县2007至2009年每年的旅游收入及旅游人数(其中缺少2009年入境旅游人数)的有关数据,整理并分别绘成图1,图2.
为了了解延庆的旅游情况,小明收集了延庆县2007至2009年每年的旅游收入及旅游人数(其中缺少2009年入境旅游人数)的有关数据,整理并分别绘成图1,图2.
|
|||
|
|||
|
年份 |
2007年 |
2008年 |
2009年 |
|
年旅游收入 (亿元) |
|
54 |
90 |

根据上述信息,回答下列问题:
(1)请你根据以上的信息补全 旅游收入表
(请把结果填在答题卡上),并计算该地
区2007至2009年四年的年旅游收入的
平均数是 亿元;
(2)据了解,该地区2008年、2009年旅游人数
的年增长率相同,那么2009年旅游人数是 万;
并根据以上的信息,补全图2;
(3)结合统计图和统计表,给县旅游局提一点积极的意见或建议.
19. 如图,在梯形
如图,在梯形 中,
中, ∥
∥ ,
, ,过
,过
点 作
作 ,交
,交 的延长线于点
的延长线于点 ,且
,且
 °,
°,
求 的长.
的长.
 20.如图,
20.如图, 为⊙
为⊙ 的直径,
的直径, 平分
平分 交⊙
交⊙ 于点
于点 ,
,
 的延长线于点
的延长线于点 ,
, 交
交 的延长
的延长
线于点 ,
,
(1)求证: 是⊙
是⊙ 的切线;
的切线;
(2)若 ⊙
⊙ 的半径为5,求
的半径为5,求 的长.
的长.
18. 列方程或方程组解应用题:
4月3日是首都第26个全民义务植树日,全民义务植树运动开展以来,我县大力实施工程造林及开展全民义务植树等社会造林活动,取得了显著成效。今年,市政公司为绿化西湖沿河风光带,计划购买五角枫、洋槐两种树苗共500株,五角枫每株50元,洋槐每株80元 .若购买树苗预计用37000元,求五角枫、洋槐两种树苗各购买多少株?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com