20. 已知x,y为正实数,且满足关系式x²-2x+4y²=0,求x的最大值.

19.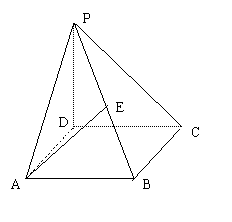 (改编)如图所示，PD垂直正方形ABCD所在的平面，AB=2，E是PB的中点，=

　 (1).建立适当的空间坐标系,写出点E的坐标.

　 (2).在平面PAD内求一点F,使EF.

18.从原点出发的某质点M, 按向量=(0,1)移动的概率为,按向量=(0,2)移动的概率为,设可达到点(0,n)的概率为P_n,

求： (1).求P₁和P₂的值.

　(2).求证:P_n+2=P_n+P_n+1.

　(3).求P_n的表达式.

17. 设关于x的函数y=2cos²x-2acosx-(2a+1)的最小值为f(a).

　　　 求： (1).写出f(a)的表达式；

　　　　 (2).试确定能使f(a)=的a的值,并求此时函数y的最大值.

16．(自编)给出下列五个命题：

　　 ①有两个对角面是全等的矩形的四棱柱是长方体。

②函数y=sinx在第一象限内是增函数。

③f(x)是单调函数，则f(x)与f^-1(x)具有相同的单调性。

④一个二面角的两个平面分别垂直于另一个二面角的两个平面，则这两个二面角的平面角互为补角。

⑤当椭圆的离心率e越接近于0时，这个椭圆的形状就越接近于圆。

　其中正确命题的序号为　　　　　　 。

15. m为大于1且小于10的正整数,若(^m的展开式中有不含x的项，满足这样条件的m有　　　　　　 个。

13．若向量=(3,2),且,则点B的轨迹方程是　　　　 　.

14 函数f(x)=(a>0且a,若f(x₁)-f(x₂)=2,则f(x₁³)-f(x₂³)= 　　　.

12. 一个机器猫每秒前进或后退一步，程序设计人员让机器猫以每前进3步，然后再后退2步的规律移动；如果将此机器猫放在数轴的原点上，面向正的方向，以1步的距离为1个单位长，令P(n)表示第n秒时机器猫所在的位置的坐标，且P(0)=0，那么下列结论中错误的是　　　　　　　　　　　　　　　　　　 　　(　　 )

　　 A. P(3)=3　　　 B. P(5)=1　　 C. P(101)=21　　　 D. P(103)<P(104)

10.已知棱长为1的正方体容器ABCD-A₁B₁C₁D₁，在棱AB，BB₁以及BC₁的中点处各有一个小孔E、F、G，若此容器可以任意放置，则该容器可装水的最大容积为(　　 )

　　　　 A．　　　　 B.　　　　 C. 　　　　　D.

11已知x,y ,且x+2y≥1,则二次函数式u=x²+y²+4x-2y的最小值为。　　　　 (　 )

　　　 　　A．-3　 　　　　B. 　　　　　C. 24　　　　　　　　 D.

9.椭圆ax²+by²=1与直线y=1-x交于A、B两点，过原点与线段AB中点的直线的斜率为，则的值为　　 　　　　　　　　　　　　　　　　　　　　(　　 )

　　　 A. 　　　B.　　　 C. 　　　　D.