5.一定质量的气体，在压强不变的条件下，体积增大，则

A.气体分子的平均动能增大

B.气体分子的平均动能减少

C.气体分子的平均动能不变

D.条件不够，无法判定气体分子平均动能的变化

[解析] 根据气体状态参量间的定性关系，在压强不变时，体积增大，则温度升高，气体分子平均动能增大.A选项正确.

[答案] A

4.封闭在玻璃容器内的气体，温度升高时不变的物理量是(不计容器的体积变化)

A.分子的平均动能　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 B.分子的平均速率

C.气体的压强　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 D.气体的密度

[解析] 封闭玻璃容器的容积不变，气体的体积不变，密度不变.D选项正确.

[答案] D

3.有甲、乙两种气体，如果甲气体内分子的平均速率大于乙气体内分子的平均速率，则

A.甲的温度一定高于乙的温度

B.甲的温度一定低于乙的温度

C.甲的温度一定等于乙的温度

D.甲的温度可能低于乙的温度

[解析] 甲气体内分子的平均速率大于乙气体内分子的平均速率，但甲气体内分子的平均动能可能小于乙气体内分子的平均动能，所以，甲的温度可能低于乙的温度.

[答案] D

2.温度相同的氧气和氢气，它们的分子平均动能之比为

A.1∶1　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 B.8∶1

C.1∶8　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 D.无法确定

[解析] 温度是分子平均动能的量度，氧气和氢气的温度相同，则分子平均动能相同.

[答案] A

1.关于绝对零度的说法中，正确的是

A.气体在绝对零度附近所有分子都将停止运动

B.绝对零度就是冰水混合物的温度

C.用摄氏温标来表示，绝对零度的数值为－273 ℃

D.随着低温技术的发展，绝对零度是可能达到的

[解析] 绝对零度时所有物质的分子都将停止运动，它是低温的极限，是永远达不到的.在温度降低到接近绝对零度之前，所有的气体都早已液化.

[答案] C

2.连通器模型

如图8-2-3所示，U形管竖直放置.根据帕斯卡定律可知，同一液体中的相同高度处压强一定相等.所以气体B和A的压强关系可由图中虚线所示的等高线联系起来.则有：

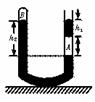
图8-2-3

p_B+ρgh₂=p_A

而p_A=p₀+ρgh₁,所以气体B的压强为：

p_B=p₀-ρg(h₂-h₁),其实该类问题与“活塞模型”并没有什么本质的区别.熟练后以上压强的关系式均可直接写出，不一定均从受力分析入手.

●典例剖析

［例1］如图8-2-4所示，在竖立的绝热容器中，隔板将气体分为A和B两部分，两部分气体的密度ρ_A＜ρ_B.若抽开隔板，当两部分气体均匀混和后，全部气体的内能将

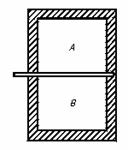
图8-2-4

A.增加　　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　 B.减小

C.不变　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 D.不能判定

[解析] 当抽开隔板后，气体将从密度大的B向密度小的A扩散.当达到动平衡时，整个气体的重心将升高，因此重力势能增加.

根据能量守恒和转化定律，在绝热的条件下，系统增加的重力势能等于减少的内能.所以，气体的内能减少，温度降低--应选答案B.

[设计意图] 本例反映的是机械能和气体内能的转的过程，通过本例说明利用能量守恒定律分析气体内能变化问题的方法.

［例2］在一标准大气压(相当于76 cm水银柱产生的压强)下做托里拆利实验时，由于管中混入少量空气，水银柱上方有一节空气柱，如图8-2-5所示，这时管中稀薄气体的压强相当于下列哪个数据的水银柱产生的压强

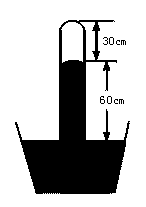
图8-2-5

A.60 cm　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 B.30 cm

C.16 cm　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 D.46 cm

[解析] 托里拆利管中混入空气后，水银上方已不是真空，这时内外液面的高度差也不再等于大气压强，而变成了管内外气体的压强差.所以稀薄气体的压强为:

p=p₀-p_h=(76-60) cmHg=16 cmHg

所以正确的选项为C.

[设计意图] 通过本例说明气体压强的计算方法.

^※［例3］如图8-2-6，导热气缸开口向下，内有气体，缸内活塞可自由滑动且不漏气，活塞下挂一个砂桶，砂桶装满砂子时，活塞恰好静止，现在把砂桶底部钻一个小洞，细砂慢慢漏出，并缓慢降低气缸外部环境温度，则

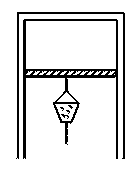
图8-2-6

A.气体压强增大，内能可能不变

B.外界对气体做功，气体温度可能降低

C.气体体积减小，压强增大，内能一定减小

D.外界对气体做功，气体内能一定增加

[解析] 要正确解答本题必需抓住几个关键的词句.“细砂慢慢漏出”“缓慢降低”温度、“导热气缸”所隐含的内容为：活塞受力平衡，则内部气体压强增大，(P=P₀-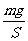);缸内气体温度逐渐降低，则气体内能减小.细砂慢慢漏出的过程中，由活塞的受力情况可知，缸内气体的压强逐渐增大，又因为内部气体温度随外界温度的降低而降低，所以活塞将缓慢上升.其功能的转化情况是：外界对气体做功，气体对外放热，气体内能减小.所以正确的选项为C.

[说明] 热平衡与力平衡的含义完全不同.热平衡指的是温度相同，而力平衡指的是合外力为零.若本题中的气缸是绝热的，那么答案又如何呢？

[设计意图] 通过本例说明综合应用热力学第一定律、气体内能的特点、气体状态参量的定性关系分析问题的方法.

●反馈练习

★夯实基础

1.活塞模型

如图8-2-1和8-2-2是最常见的封闭气体的两种方式.图8-2-1中活塞的质量为m，气缸横截面积为S，外界大气压强为P₀.由于活塞处于平衡状态，所以

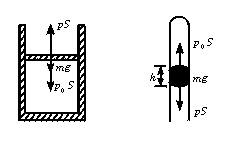
图8-2-1　　　　 图8-2-2

p₀S+mg=pS

则气体的压强为：

p=p₀+.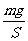

其实图8-2-2中的液柱也可以看成一个活塞，由于液柱处于平衡状态，所以

pS+mg=p₀S

则气体压强为：

p=p₀-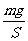=p₀-ρgh.

总之，对“活塞模型”类求压强的问题，其基本的方法就是先对“活塞”受力分析，然后根据平衡条件或牛顿第二定律列方程.(请同学们思考：若图8-2-1中的气缸整体具有向上的加速度a,被封气体的压强如何表示？)

3.气体压强的微观解释

气体的压强是大量气体分子频繁地碰撞器壁而产生的.气体的压强就是大量气体分子作用在器壁单位面积上的平均作用力.气体分子的平均动能越大，分子越密，对单位面积器壁产生的压力就越大，气体的压强就越大.

●疑难解析

气体压强的确定

2.气体分子速率分布的统计规律

大量分子做无规则运动，速率有的大，有的小，但大多数分子的速率都在某个数值附近，离开这个数值越远，分子数越少，表现出“中间多，两头少”的规律.温度升高时，速率大的分子数增加，分子的平均速率增大.

1.气体分子运动的特点

气体中的分子虽然比较稀疏，但是，每 cm³体积内的分子数仍有10¹⁹个，1个空气分子在1 s内与其他空气分子的碰撞次数竟达10⁹次之多.就某一个分子来说，它在某一时刻的速度具有怎样的大小和方向，完全是偶然的，但对大量分子的整体来说，分子的运动却表现出一定的规律.