18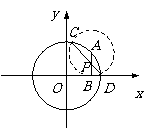．解　 设点A的坐标为A(2cosa，2sina)，

则以A为圆心、AB为半径的圆的方程为

(x－2cosa)² + (y－2sina)² = 4sin²a． ……… 4分

联立已知圆x² + y² = 4的方程，相减，

可得公共弦CD的方程为

xcosa + ysina = 1+ cos²a．　　　　　　 (1) ………　 8分

而AB的方程是　 x = 2cosa．　　　　　 (2)

所以满足(1)、(2)的点P的坐标为(2cosa，sina)，消去a，即得

点P的轨迹方程为x² + 4y² = 4．　　　　　　　 　………………　 12分

说明： 设A(m，n)亦可类似地解决．

17．解　 ∵　 对任意nÎN^*，有 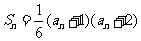，　　 (1)

∴　 当n=1时，有　 ，

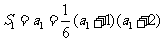解得　 a₁ = 1 或a₁ = 2．　　　　　　　　　　　　　　　　　 ………………　 3分

当n≥2时，有 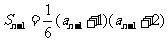．　　　　　　 　　　　(2)

于是，由 (1)－(2) 整理可得　 (a_n + a_n－1)(a_n－a_n－1－3)=0．

因为{a_n}的各项均为正数，所以　 a_n－a_n－1 = 3．　 ……………　 8分

当a₁ = 1时，a_n =1+3(n－1)=3n－2，此时a₄²=a₂a₉成立．

当a₁ = 2时，a_n =2+3(n－1)=3n－1，此时a₄²=a₂a₉不成立，故a₁=2舍去．

所以a_n=3n－2．　 　　　　　　　　　　　　　　　　　　　　………………　 12分

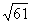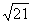13．2 　　　　14．二或四　　　 15．或　　　 16．

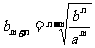
CABC　　 BADD　　 CBDA

22．(本题满分14分)　 试利用“对数函数y = log _a x在(0，+∞)上的单调性质：0＜x₁＜x₂ Û log _a x₁＜log _a x₂ (a＞1)；0＜x₁＜x₂ Û　 log _a x₁＞log _a x₂ (0＜a＜1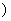” 解决下列问题：

已知二次函数f(x)的图象开口向下,且对任意实数x有f(2－x)=f(2+x), 解关于x的不等式：

．

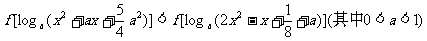紫马一中2010届高三下学期第二次模拟考试(数学)

参考解答及评分标准

21．(本题满分12分) 证明： ．

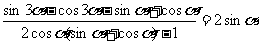20．(本题满分12分) 某地计划从今年起填湖围造一部分生产和生活用地.若填湖费、购置排水设备费等所需经费与当年所填湖造地面积x (亩)的平方成正比，其比例系数为a．设每亩水面的年平均经济收益为b元，填湖造地后的每亩土地的年平均收益为c元(其中a，b，c均为常数)．

(Ⅰ) 若按计划填湖造地，且使得今年的收益不小于支出，试求所填面积x的最大值．

(Ⅱ) 如果填湖造地面积按每年1%的速度减少，为保证水面的畜洪能力和环保要求，填湖造地的总面积永远不能超过现有水面面积的25%，求今年填湖造地的面积最多只能占现有水面的百分之几.

19．(本题满分12分) 设平面内的向量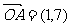, , 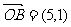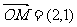，点P是直线OM上的一个动点，求当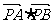取最小值时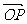，的坐标及ÐAPB的余弦值．

18．(本题满分12分) 已知A是圆x² + y² = 4上任一点，AB垂直于x轴，交x轴于点B．以A为圆心、AB为半径作圆交已知圆于C、D，连结CD交AB于点P，求点P的轨迹方程．

17．(本题满分12分) 已知数列{a_n}的各项均为正数，且前n项和S_n满足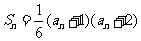．若a₂、a₄、a₉ 成等比数列，求数列{a_n}的通项公式．