2.health　 　　　　　　　 A. reach　　 　　　　　　　 B. heat　　　　 　　 C. heaven　　 　　　　　　　 D. cheap

第一节 语音知识(共5小题；每小题1分，满分5分)

1.pound　 　　　　　　 A. thought　 　　　　　 B. southern　 　　　　 C. through　 　 　　　 D. thousand

22．(本小题满分14分)

已知定义在实数集R上的函数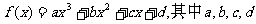是实数.

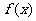　 (1)若函数在区间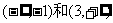上都是增函数，在区间(－1，3)上是减函

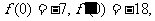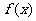数，并且求函数的表达式；

　 (2)若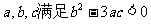，求证：函数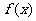是单调函数.

云南大学附属中学2010届高三下学期第二次模拟考试

21．(本小题满分12分)

F₁、F₂分别是双曲线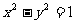的两个焦点，O为坐标原点，圆O是以F₁F₂为直径的

圆，直线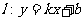与圆O相切，与双曲线交于A、B两点.

　 (1)根据条件求出b和k满足的关系式；

　 (2)当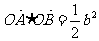时，求直线l的方程；

20．(本小题满分12分)

已知数列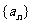，设S_n是数列的前n项和，并且满足a₁=1，对任意正整数n，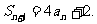

　 (1)令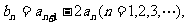证明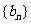是等比数列，并求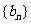的通项公式；

　 (2)令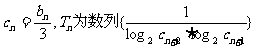的前n项和，求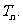

19．(本小题满分12分)

如图所示，已积压四棱锥P-ABCD的底面是直角梯形，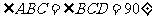

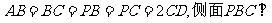　 底面ABCD.

　 (1)证明：；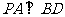

　 (2)求二面角P-BD-C的大小；

　 (3)求证：平面平面PAB.

18．(本小题满分12分)

　　 一名学生在军训中练习射击项目，他射击一次，命中目标的概率是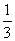，若连续射击

6次，且各次射击是否命中目标相互之间没有影响.

　 (1)求这名学生在第3次射击时，首次命中目标的概率；

　 (2)求这名学生在射击过程中，恰好命中目标3次的概率.

17．(本小题满分12分)

已知函数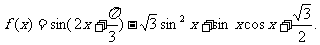

　 (1)求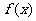的最小正周期；

　 (2)求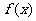的最小值及此时x的值；

　 (3)求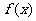的单调递增区间.

16．下面有四个命题：

①若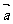、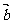为一平面内两非零向量，则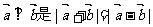的充要条件；

②一平面内两条曲线的方程分别是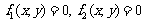，它们的交点是，

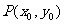则方程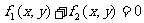的曲线经过点P；

③经过一定点且和一条已知直线垂直的所有直线都在同一平面内；

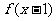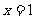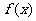④若函数的图象关于直线对称，则为偶函数.

其中真命题的序号是　　　　　　 (把符合要求的命题序号都填上).

15．直线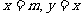将圆面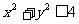分成若干块. 现在用5种不同的颜色给这若干块涂

色，每块只涂一种颜色，且任意两块不同色，若共有120种不同的涂法，则实数m的取

值范围是　　　　　　　　　　　 .