
7、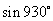 的值是
( )
的值是
( )
(A)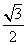 (B)
(B)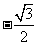 (C)
(C)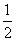 (D)
(D)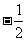
6、(08江苏模拟)已知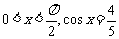 ,则
,则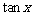 =
.
=
.
5、(07浙江文2)已知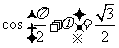 ,且
,且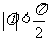 ,则tan
,则tan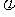 = ( )
= ( )
(A)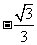 (B)
(B) 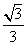 (C) -
(C) -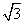 (D)
(D) 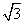
4、(07湖北文1)tan690°的值为 ( )
A.-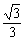 B.
B.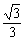 C.
C.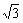 D.
D.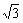
3、(07全国2文1)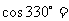 ( )
( )
A.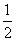 B.
B.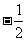 C.
C.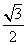 D.
D.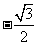
2、(07全国2 理1)sin2100 = ( )
A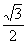 B-
B-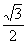 C
C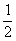 D
-
D
-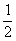
1、(07全国1文2)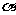 是第四象限角,
是第四象限角,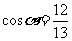 ,则
,则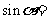 (
)
(
)
A.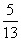 B.
B.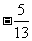 C.
C. 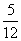 D.
D.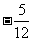
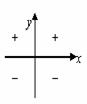
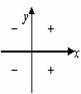
5. 各象限角的各种三角函数值符号:一全二正弦,三切四余弦
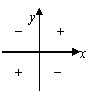
典型例题
EG1、写出与下列各角终边相同的角的集合S,并把S中适合不等式-3600≤β<7200的元素β写出来:
(1)600; (2)-210; (3)363014,
变式1、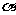 的终边与
的终边与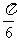 的终边关于直线
的终边关于直线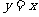 对称,则
对称,则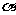 =_____。
=_____。
EG2、三角函数线问题
若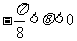 ,则
,则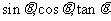 的大小关系为_____
的大小关系为_____
变式1、若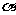 为锐角,则
为锐角,则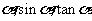 的大小关系为_______
的大小关系为_______
变式2、函数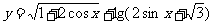 的定义域是_______
的定义域是_______
EG3、.已知2弧度的圆心角所对的弦长为2,那么这个圆心角所对的弧长为( )
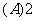
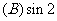
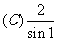
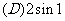
变式1、已知扇形AOB的周长是6cm,该扇形的中心角是1弧度,求该扇形的面积。
变式2.某扇形的面积为1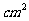 ,它的周长为4
,它的周长为4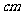 ,那么该扇形圆心角的度数( )
,那么该扇形圆心角的度数( )
A.2° B.2 C.4° D.4
变式3.中心角为60°的扇形,它的弧长为2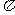 ,则它的内切圆半径为( )
,则它的内切圆半径为( )
A.2 B.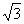 C.1 D.
C.1 D.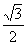
变式4.一个半径为R的扇形,它的周长为4R,则这个扇形所含弓形的面积为( )
A.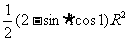 B.
B.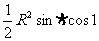
C.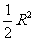 D.
D.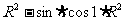
变式5.已知扇形的半径为R,所对圆心角为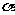 ,该扇形的周长为定值c,则该扇形最大面积为
.
,该扇形的周长为定值c,则该扇形最大面积为
.
EG4、 已知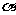 为第三象限角,则
为第三象限角,则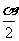 所在的象限是( )
所在的象限是( )
(A) 第一或第二象限 (B)第二或第三象限(C)第一或第三象限(D)第二或第四象限
变式1、若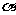 是第二象限角,则
是第二象限角,则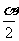 是第_____象限角。
是第_____象限角。
变式2、若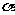 角的终边落在第三或第四象限,则
角的终边落在第三或第四象限,则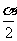 的终边落在( )
的终边落在( )
A.第一或第三象限 B.第二或第四象限
C.第一或第四象限 D.第三或第四象限
EG5、已知角a的终边经过P(4,-3),求2sina+cosa的值.
变式1、(08北京模拟)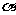 是第四象限角,
是第四象限角, ,则
,则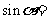 ( ).
( ).
A.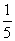 B.
B.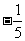 C.
C.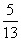 D.
D.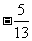
变式2、已知角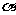 的终边经过点P(5,-12),则
的终边经过点P(5,-12),则 的值为__。
的值为__。
变式3、设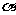 是第三、四象限角,
是第三、四象限角,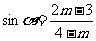 ,则
,则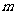 的取值范围是_______
的取值范围是_______
EG6.若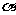 是第三象限角,且
是第三象限角,且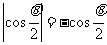 ,则
,则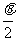 是( )
是( )
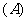 第一象限角
第一象限角  第二象限角
第二象限角  第三象限角
第三象限角  第四象限角
第四象限角
变式1、(08江西)在复平面内,复数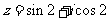 对应的点位于
对应的点位于
A.第一象限 B.第二象限 C.第三象限 D.第四象限
EG7、若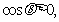
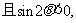
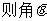 的终边所在象限是( )
的终边所在象限是( )
A第一象限 B第二象限 C第三象限 D第四象限
变式1、(07北京文理1)已知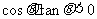 ,那么角
,那么角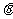 是( )
是( )
A.第一或第二象限角 B.第二或第三象限角
C.第三或第四象限角 D.第一或第四象限角
变式2.(08全国Ⅱ1)若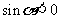 且
且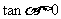 是,则
是,则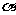 是( C )
是( C )
A.第一象限角 B. 第二象限角 C. 第三象限角 D. 第四象限角
实战训练
4.三角函数定义:
利用直角坐标系,可以把直角三角形中的三角函数推广到任意角的三角数.在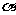 终边上任取一点
终边上任取一点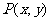 (与原点不重合),记
(与原点不重合),记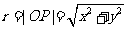 ,
,

则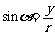 ,
,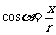 ,
,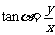 ,
,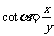 。
。
注: ⑴三角函数值只与角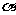 的终边的位置有关,由角
的终边的位置有关,由角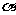 的大小唯一确定,
的大小唯一确定,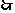 三角函数是以角为自变量,以比值为函数值的函数.
三角函数是以角为自变量,以比值为函数值的函数.
⑵根据三角函数定义可以推出一些三角公式:
①诱导公式:即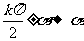 或
或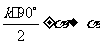 之间函数值关系
之间函数值关系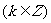 ,其规律是“奇变偶不变,符号看象限”
;如
,其规律是“奇变偶不变,符号看象限”
;如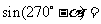
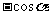
②同角三角函数关系式:平方关系,倒数关系,商数关系.
⑶重视用定义解题.
⑷三角函数线是通过有向线段直观地表示出角的各种三角函数值的一种图示方法.如单位圆
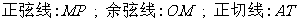
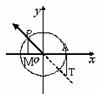
3.弧度制下的公式
扇形弧长公式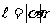 ,扇形面积公式
,扇形面积公式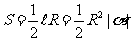 ,其中
,其中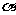 为弧所对圆心角的弧度数。
为弧所对圆心角的弧度数。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com