
19.(本小题满分13分)
已知函数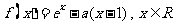 .
.
(1)若实数 ,求函数
,求函数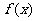 在
在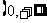 上的极值;
上的极值;
(2)记函数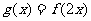 ,设函数
,设函数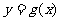 的图象C与
的图象C与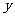 轴交于
轴交于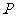 点,曲线C在
点,曲线C在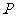 点处的切线与两坐标轴所围成的图形的面积为
点处的切线与两坐标轴所围成的图形的面积为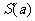 ,求当
,求当 时
时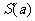 的最小值。
的最小值。
18.(本小题满分12分)
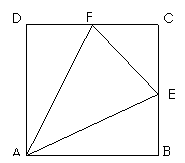
 已知四边形
已知四边形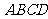 是边长为
是边长为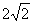 的正方形,
的正方形,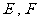 分别为
分别为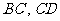 的中点,沿
的中点,沿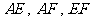 将
将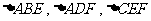 向同侧折叠且与平面
向同侧折叠且与平面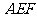 成直二面角,连接
成直二面角,连接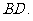
(1)求证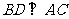 ;
;
(2)求平面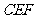 与平面
与平面 所成锐角的余弦值。
所成锐角的余弦值。
17.(本小题满分12分)
上海世博会于2010年5月1日正式开幕,按规定个人参观各场馆需预约,即进入园区后持门票当天预约,且一张门票每天最多预约六个场馆。考虑到实际情况(排队等待时间等),张华决定参观甲、乙、丙、丁四个场馆。假设甲、乙、丙、丁四个场馆预约成功的概率分别是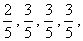 且它们相互独立互不影响。
且它们相互独立互不影响。
(1)求张华能成功预约甲、乙、丙、丁中两个场馆的概率;
(2)用 表示能成功预约场馆的个数,求随机变量
表示能成功预约场馆的个数,求随机变量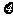 的分布列和数学期望。
的分布列和数学期望。
16.(本小题满分12分)
已知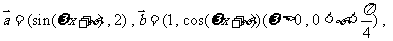 函数
函数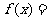

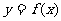 的图象的相邻两对称轴之间距离为2,且过点
的图象的相邻两对称轴之间距离为2,且过点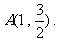
(1)求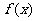 的表达式;
的表达式;
(2)求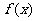 的单调递增区间。
的单调递增区间。
15.给出以下几个命题:
①已知函数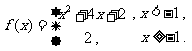 则
则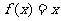 有三个根;
有三个根;
②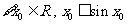 ;
;
③过空间任一点,有且只有一个平面与两异面直线同时平行;
④两条直线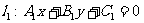 与直线
与直线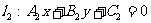 平行的充要条件是
平行的充要条件是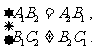
⑤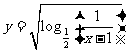 的定义域是
的定义域是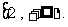
则正确的命题有 (填序号)。
14.在锐角 中,
中,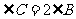 ,则
,则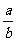 的取值范围是
的取值范围是
13.已知 ,则
,则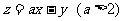 的取值范围是
。
的取值范围是
。
12.数列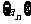 的前
的前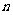 项和为
项和为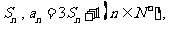 则
则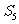 为
。
为
。
11.在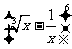 的展开式中
的展开式中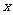 的指数是整数的项共有 项。
的指数是整数的项共有 项。
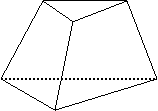
10.从足够多的四种颜色的灯泡中任选六个安置在如右图的6个顶点处,则相邻顶点处灯泡颜色不同的概率为 ( )
 A.
A.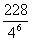 B.
B.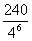 C.
C.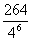 D.
D.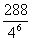
第Ⅱ卷(满分100分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com