
4. 已知向量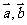 满足
满足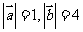 ,且
,且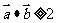 ,则
,则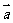 与
与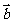 的夹角的取值范围是 ( )
的夹角的取值范围是 ( )
A.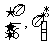 B.
B.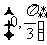 C.
C.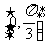 D.
D.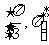
3. 函数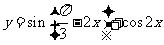 的最小正周期是
( )
的最小正周期是
( )
A.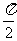 B.
B.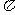 C.
C.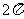 D.
D.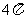
2. 已知复数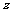 满足
满足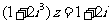 ,则
,则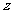 等于 ( )
等于 ( )
A.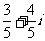 B.
B. 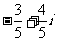 C.
C.
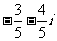 D.
D. 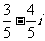
1. 设全集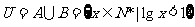 ,若
,若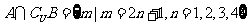 ,
,
则集合B= ( )
A.{2,4,6,8} B.{2,4,6,8,10} C.{1,2,4,6,8} D.{3,5,7,9}
22.(本题满分14分)已知 处有极值,其图象在x=1处的切线与直线6x+2y+5=0平行.
处有极值,其图象在x=1处的切线与直线6x+2y+5=0平行.
(1)求函数的单调区间;
(2)求函数的极大值与极小值的差;
(3)若x 求实数c的取值范围.
求实数c的取值范围.
贵州大学附属中学2010届高三下学期二模数学试题
21.(本题满分12分)已知双曲线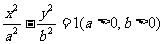 的左、右焦点分别是F1、F2,点P在双曲线的右支上,且|PF1|=3|PF2|
的左、右焦点分别是F1、F2,点P在双曲线的右支上,且|PF1|=3|PF2|
(1)求双曲线的离心率的最大值及此时渐近线方程;
(2)当P的坐标为(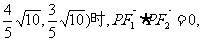 求双曲线的方程.
求双曲线的方程.
20.(本题满分12分)从原点出发的某质点M,按向量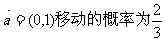 ,按向量
,按向量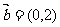 移动的概率为
移动的概率为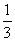 ,设M可到达点(0,n)的概率为Pn.
,设M可到达点(0,n)的概率为Pn.
(1)求P1和P2的值;
(2)求证: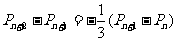 ;
;
(3)求Pn的表达式.
19.(本题满分12分)如图所示,设四边形ABCD是矩形,PA⊥平面ABCD,E、F分别是AB、PD的中点.
(1)求证:AF//平面PCE;
(2)若二面角P-CD-B为45°,求二面角E-PC-D大小;
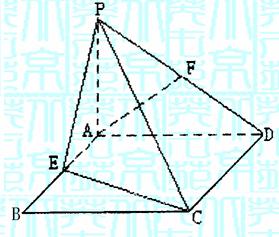 (3)在(2)的条件下,若AD=2,CD=3,求点F到平面PCE的距离.
(3)在(2)的条件下,若AD=2,CD=3,求点F到平面PCE的距离.
18.(本题满分12分)在△ABC中,角A、B、C所对边分别是a、b、c,且a2<b2+c2,
且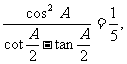 求cosA-sinA的值.
求cosA-sinA的值.
17.(本题满分12分)设F是椭圆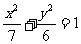 的右焦点,且椭圆上至少有21个不同的点
的右焦点,且椭圆上至少有21个不同的点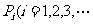 ),使|FP1|、|FP2|、|FP3|、…组成公差为d的等差数列,求公差d的取值范围.
),使|FP1|、|FP2|、|FP3|、…组成公差为d的等差数列,求公差d的取值范围.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com