7、若函数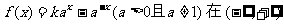上既是奇函数，又是增函数，则

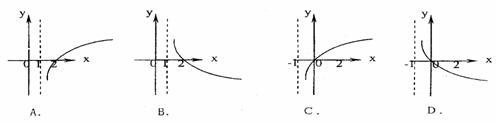
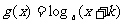的图像是

6、现向一个半径为R的球形容器内匀速注入某种液体，下面图形中能表示在注入过程中容器的液面高度h随时间t的函数关系的是(　)

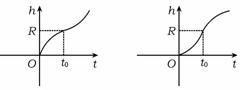
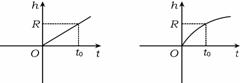
　　　　　　　 A　　　　　　　　　　 B　　 　　　　　　C　　 　　　　　　　

5、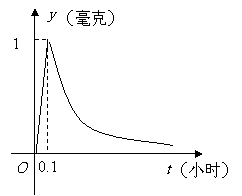为了预防流感，某学校对教室用药熏消毒法进行消毒．已知药物释放过程中，室内每立方米空气中的含药量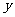(毫克)与时间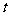(小时)成正比；

药物释放完毕后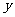，与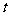的函数关系式为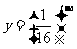(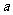为常数)，如图所示．

据图中提供的信息，回答下列问题：

(I)从药物释放开始，每立方米空气中的含药量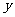(毫克)与时间　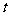 　　(小时)之间的函数关系式为 　　　　　　　　　　 ；

(II)据测定，当空气中每立方米的含药量降低到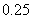毫克以下时，学生方可进教室，那么， 药物释放开始，至少需要经过　　　　 小时后，学生才能回到教室．

4、若函数f(x)的反函数为f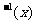,则函数f(x-1)与f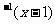的图象可能是

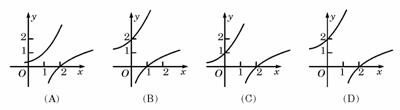
3、函数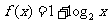与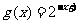在同一直角坐标系下的图象大致是(　)

6、方程f(x,y)=0的曲线过点(2，4)，则方程f(2－x,y)=0的曲线必过点　　　　　 　　

典型例题

EG1．讨论函数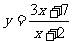的图象与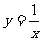的图象的关系。

EG2．图①是某公共汽车线路收支差额y元与乘客量x的图象.

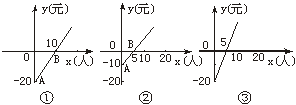
(1)试说明图①上点A、点B以及射线AB上的点的实际意义.

(2)由于目前本条线路亏损，公司有关人员提出了两种扭亏为赢的建议，如图②③所示.你能根据图象，说明这两种建议的意义吗？

(3)图①、图②中的票价是多少元？图③中的票价是多少元？票价在图中的几何意义是什么?

EG3．(1)若方程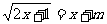有两个不同的实数根，求实数m的范围。

(2)求不等式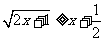的解；

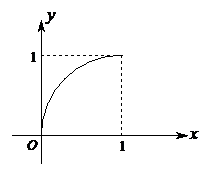EG4、已知定义在区间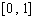上的函数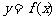的图像如图所示，对于满足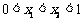的任意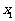、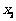，给出下列结论：

①　　 ；

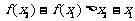②　　 ；

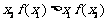③　　 ．

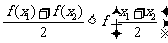其中正确结论的序号是　　　　．(把所有正确结论的序号都填上)　　　　　　　　　　　　　

EG5.已知函数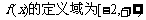，且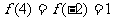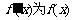，的导函数，函数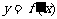的图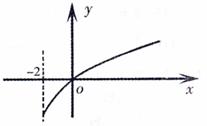象如图所示. 则平面区域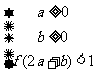所围成的面积是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

　 A．2　　　　　　　　　　　　　　 B．4 　　　　　　　　　　 C．5　　　　　　　　　　　 D．8

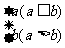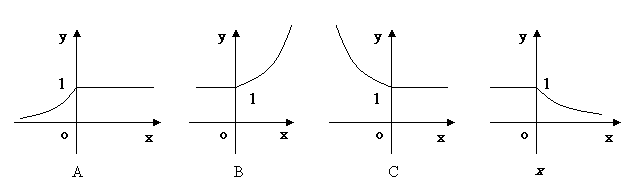
EG6．定义运算ab=，则函数f(x)=12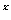 的图象是(　　 )。

EG7．如图2所示，函数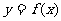的图象在点P处的切线方程是

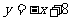，则　　　　 ，　　　　 ．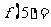　　　

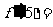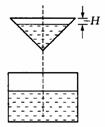EG8．如图所示，液体从一圆锥形漏斗漏入一圆柱形桶中，开始时，漏斗盛满液体，经过3分钟漏完．已知圆柱中液面上升的速度是一个常量，H是圆锥形漏斗中液面下落的距离，则H与下落时间t(分)的函数关系表示的图象只可能是(　 　)．

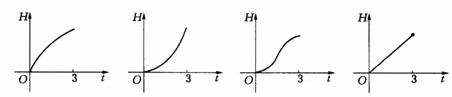
　　　　 A．　　　B．　　　C．　　　　D．

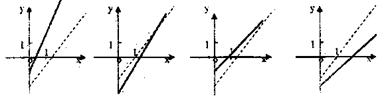
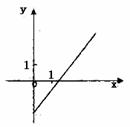　 　 EG9．右图是某公交线路收支差额y与乘客量x之间的关系图(收支差额=车票收入+财政补贴-支出费用；假设财政补贴和支出费用与乘客量无关)，在这次公交、地铁票价听证会上，有市民代表提出“增加财政补贴，票价实行8折优惠”的建议.则下列四个图像反映了市民代表建议的是　　　　　 (　　 )

　 A．　　　　 　B．　 　　　　　C．　　　　　 D．

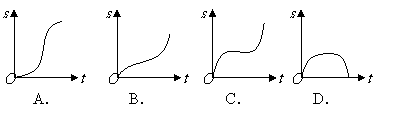
EG10．(08全国Ⅰ2)汽车经过启动、加速行驶、匀速行驶、减速行驶之后停车，若把这一过程中汽车的行驶路程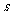看作时间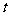的函数，其图像可能是(　 )

5、方程(a>0且a≠1)实数解的个数是　

4、函数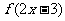的图象，可由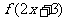的图象经过下述变换得到(　 )

A．向左平移6个单位　 　　　B．向右平移6个单位

C．向左平移3个单位　　 　　D．向右平移3个单位

3、设函数y=f(x)的定义域为R，则函数y=f(x-1)与y=f(1-x)的图象关系为　　　　 ( 　　)

A、直线y=0对称B、直线x=0对称C、直线y=1对称D、直线x=1对称