
5.三棱台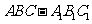 中,高
中,高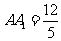 ,上底面三边长分别为
,上底面三边长分别为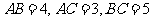 ,
,
上下底边的比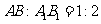 ,则侧面
,则侧面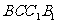 与底面所成的二面角的大小为
与底面所成的二面角的大小为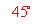 .
.
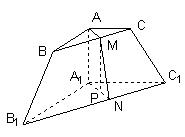
[解析]如图,作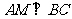 ,作
,作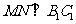 ,连
,连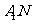 ,作
,作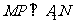 ,则
,则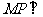 平面
平面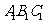 ,可以证得
,可以证得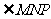 为所求的二面角的平面角.
为所求的二面角的平面角.
在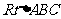 中,可求得
中,可求得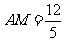 ,
,
∵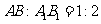 ,
,
∴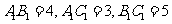 ,
,
在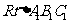 ,可求得高
,可求得高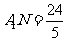 ,
,
∴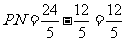 ,又
,又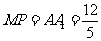 ,
,
∴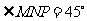 .
.
答案: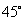
4.已知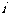 是虚数单位,
是虚数单位,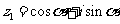 ,
,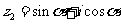 ,则
,则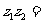
 .
.
[解析]

2.已知函数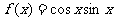
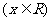 ,给出下列四个命题:
,给出下列四个命题:
①若 ,则
,则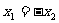 , ②
, ②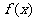 的最小正周期是
的最小正周期是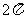 ,
,
③在区间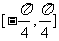 上是增函数, ④
上是增函数, ④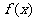 在区间
在区间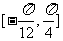 上的值域是
上的值域是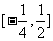 .
.
其中真命题是 ③、④ .
[解析]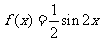 ,特殊值法检验①,由
,特殊值法检验①,由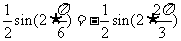 ,可知①错误;
,可知①错误;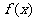 的最小正周期是
的最小正周期是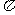 ,②错误;由图像知在区间
,②错误;由图像知在区间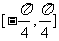 上
上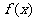 是增函数,③正确;∵
是增函数,③正确;∵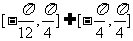 ,∴区间
,∴区间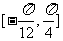 上
上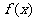 是增函数,
是增函数,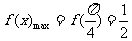 ,
,
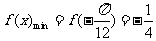 ,④正确.
,④正确.
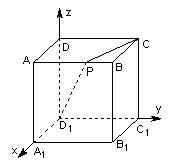
1.已知长方体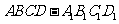 中,
中,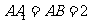 ,若棱
,若棱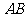 上存在点
上存在点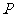 使
使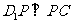 ,则棱
,则棱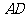 的长的取值范围是
的长的取值范围是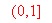 .
.
[解析]如图建立坐标系,设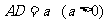 ,
,
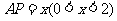 ,则
,则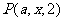 ,
,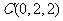 ,
,
∴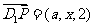 ,
,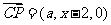 ,
,
∵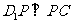 ,∴
,∴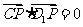 ,
,
即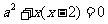 ,
,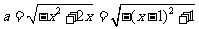 ,当
,当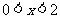 时,
时,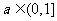 .
.
21.(本小题满分14分)
设等差数列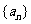 的前
的前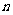 项和为
项和为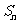 今日必看
今日必看
(1)若数列首项为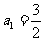 ,公差
,公差 今日必看,求满足
今日必看,求满足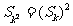 的正整数
的正整数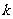 的值;今日必看
的值;今日必看
(2)若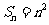 ,求通项
,求通项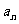 ;今日必看
;今日必看
(3)求所有等差数列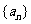 ,使得对于一切正整数
,使得对于一切正整数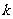 都有
都有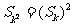 成立。今日必看
成立。今日必看
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com