
18.(本题满分12分)
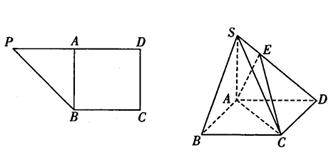
在直角梯形PBCD中,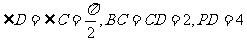 ,A为PD的中点,如下左图。将
,A为PD的中点,如下左图。将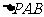 沿AB折到
沿AB折到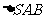 的位置,使
的位置,使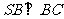 ,点E在SD上,且
,点E在SD上,且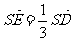 ,如下右图。
,如下右图。
(1)求证: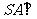 平面ABCD;
平面ABCD;
(2)求二面角E-AC-D的正切值;
 (3)在线段BC上是否存在点F,使SF//平面EAC?若存在,确定F的位置, 若不存在,请说明理由。
(3)在线段BC上是否存在点F,使SF//平面EAC?若存在,确定F的位置, 若不存在,请说明理由。
17.(本题满分12分)
已知A、B、C是三角形ABC的三内角,且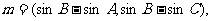
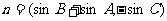 ,并且
,并且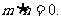
(1)求角A的大小。
(2)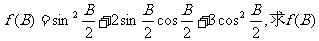 的递增区间。
的递增区间。
16.(本题满分12分)
某工厂2010年第一季度生产的A、B、C、D四种型号的产品产量用条形图表示如图,现用分层抽样的方法从中选取50件样品参加四月份的一个展销会:
(1)问A、B、C、D型号的产品各抽取多少件?
(2)从50件样品随机的抽取2件,求这2件产品恰好是不同型号产品的概率;
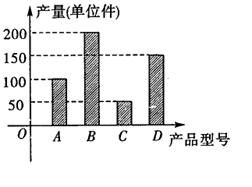
(3)从A、C型号的产品中随机的抽取3件,用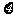 表示抽取A种型号的产品件数,求
表示抽取A种型号的产品件数,求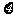 的分布列和数学期望。
的分布列和数学期望。
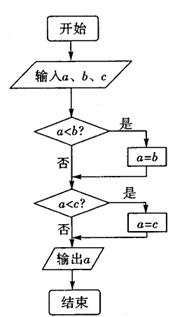
15.一个计算装置有两个数据入口I、Ⅱ与一个运算
结果输出Ⅲ,当Ⅰ、Ⅱ分别输入正整数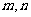 时,
时,
输出结果记为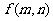 ,且计算装置运算原理如下:
,且计算装置运算原理如下:
(1)若Ⅰ、Ⅱ分别输入1,则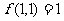 ;②若Ⅰ输入固定的正整数,输入的正整数增大1,则输出结果比原来增大3;③若Ⅱ输入固定的正整数
;②若Ⅰ输入固定的正整数,输入的正整数增大1,则输出结果比原来增大3;③若Ⅱ输入固定的正整数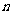 ,Ⅰ输入正整数增大1,则输出结果为原来3倍 。
,Ⅰ输入正整数增大1,则输出结果为原来3倍 。
则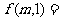 ,满足
,满足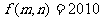 的平面上的点
的平面上的点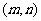 的个数是
。
的个数是
。
14.在区间[-1,1]上任取两数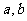 ,则二次方程
,则二次方程
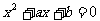 的两根都是正数的概率是
。
的两根都是正数的概率是
。
12. 已知命题
已知命题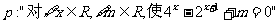 ,若命题
,若命题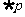 是假命题,则实数
是假命题,则实数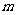 的取值范围是
。
的取值范围是
。
11.设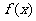 是定义在R上的以3为周期的奇函数,若
是定义在R上的以3为周期的奇函数,若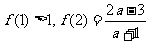 ,则实数
,则实数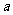 的取值范围是
。
的取值范围是
。
10.已知某曲线的参数方程为
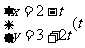 为参数),若将极点与
为参数),若将极点与
原点重合,极轴与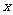 轴的正半轴重合,
轴的正半轴重合,
则该曲线的极坐标方程是 。
9.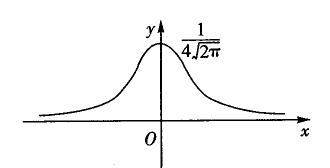 已知某正态分布的概率密度曲线
已知某正态分布的概率密度曲线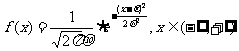 的图象如右,则函数的解析式为
的图象如右,则函数的解析式为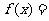 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com