
40.(15分)请考生在A、B、C三题中任选一题作答。答题时请在答题卡对应的位置上填涂作答的题号。
A.[地理--海洋地理]
读渤、黄、东海2月(甲图)和8月(乙图)多年月平均海水表面温度的空间分布图,回答下列问题。
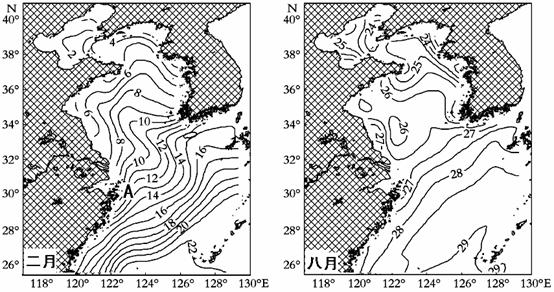
(1)说出图示海域2月和8月月平均海表面温度的分布的分布规律及其影响因素。(4分)
(2)比较渤海和东海海表面水温季节变化的差异,并分析原因。(6分)
(3)图中A海区是我国著名的渔场,简要说出该渔场形成的有利条件。(5分)
B.[地理--自然灾害与防治]
读1950-1991年间我国西北、东北、华北、
西南、长江中下游、华南等六个区域干旱季节
分布及其对农业的影响图,回答下列问题。
(1)读图指出我国干旱灾害分布特点。(3分)
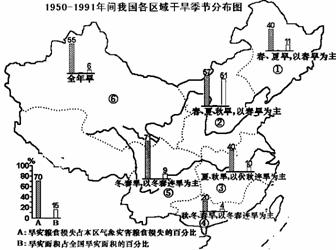 (2)2009年入秋以来,西南地区发生严重的旱灾,造成粮食作物枯死、人畜饮水困难。从长远来看,西南地区抗旱的基本措施有哪些? (8分)
(2)2009年入秋以来,西南地区发生严重的旱灾,造成粮食作物枯死、人畜饮水困难。从长远来看,西南地区抗旱的基本措施有哪些? (8分)
(3)简要分析我国东西部干旱灾害频发的主要原因。(4分)
C.[地理-环境保护]
2009年12月7-18日,世界气候大会在丹麦的哥本哈根召开。世界许多国家共同探讨如何面对全球气候变暖这一严峻课题。我国工业发展处在初级阶段,而发达国家工业发展已经进入后工业阶段。哥本哈根会议涉及各国从高碳排放的工业文明向低碳消耗的生态文明的革命性转型,世界必然走向低碳经济的绿色发展道路。
材料一:部分国家温室气体排放量比较 材料二:我国单位GDP能耗的变化状况(﹪)
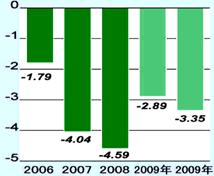

(1)读材料二,说出2006-2009年我国单位GDP能耗的变化特点。(3分)
(2)我国在节能减排,发展低碳经济方面,还需从哪些方面做出努力?(8分)
(3)近年来,某些国家指责中国排放了过多的温室气体,加剧了全球变暖,并要求我国承担更多的义务。依据以上材料并结合可持续发展的相关理论驳斥上述观点。(4分)
11.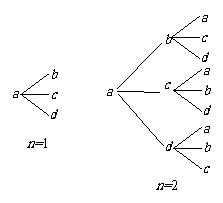 (考查:排列组合,数学归纳法,概率等)用
(考查:排列组合,数学归纳法,概率等)用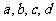 四个不同字母组成一个含
四个不同字母组成一个含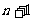
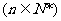 个字母的字符串,要求由
个字母的字符串,要求由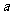 开始,相邻两个字母不同. 例如
开始,相邻两个字母不同. 例如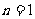 时,排出的字符串是
时,排出的字符串是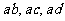 ;
;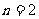 时排出的字符串是
时排出的字符串是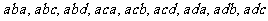 ,……,
如图所示.记这含
,……,
如图所示.记这含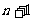 个字母的所有字符串中,排在最后一个的字母仍是
个字母的所有字符串中,排在最后一个的字母仍是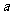 的字符串的种数为
的字符串的种数为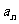 .
.
(1)试用数学归纳法证明: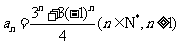 ;
;
(2)现从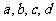 四个字母组成的含
四个字母组成的含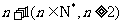 个字母的所有字符串中随机抽取一个字符串,字符串最后一个的字母恰好是
个字母的所有字符串中随机抽取一个字符串,字符串最后一个的字母恰好是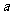 的概率为
的概率为 ,求证:
,求证: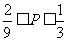 .
.
解(1):证明:
(ⅰ)当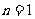 时,因为
时,因为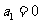 ,
,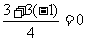 ,所以等式正确.
,所以等式正确.
(ⅱ)假设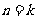 时,等式正确,即
时,等式正确,即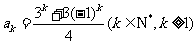 ,
,
那么,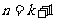 时,因为
时,因为
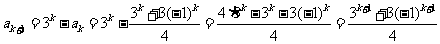 ,
,
这说明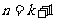 时等式仍正确.
时等式仍正确.
据(ⅰ),(ⅱ)可知,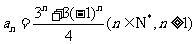 正确.
正确.
(2)易知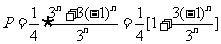 ,
,
①当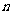 为奇数(
为奇数(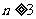 )时,
)时,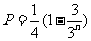 ,因为
,因为 ,所以
,所以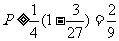 ,又
,又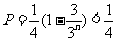 ,所以
,所以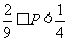 ;
;
②当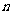 为偶数(
为偶数(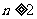 )时,
)时,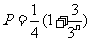 ,因为
,因为 ,所以
,所以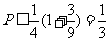 ,又
,又 ,所以
,所以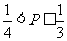 .综上所述,
.综上所述,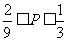 .
.
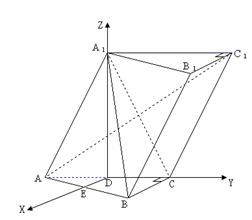
11.已知斜三棱柱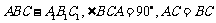 ,,
,,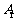 在底面
在底面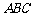 上的射影恰为
上的射影恰为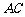 的中点
的中点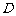 ,又知
,又知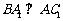 。
。
(I)求证: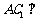 平面
平面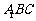 ; (II)求求二面角
; (II)求求二面角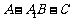 余弦值的大小
余弦值的大小
[解](I)如图,取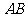 的中点
的中点 ,则
,则 ,因为
,因为 ,
,
 所以
所以 ,又
,又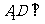 平面
平面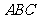 ,
,
以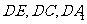 为
为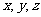 轴建立空间坐标系,
轴建立空间坐标系,
则 ,
,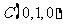 ,
,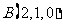 ,
,
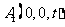 ,
,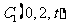 ,
,
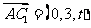 ,
,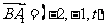 ,
,
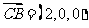 ,由
,由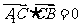 ,知
,知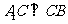 ,
,
又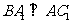 ,从而
,从而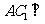 平面
平面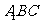 ;
;
(II)由
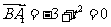 ,得
,得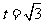 。
。
设平面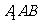 的法向量为
的法向量为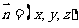 ,
,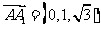 ,
,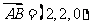 ,所以
,所以
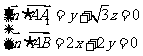 ,设
,设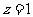 ,则
,则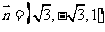
所以点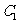 到平面
到平面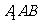 的距离
的距离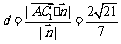 。
。
(III)再设平面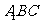 的法向量为
的法向量为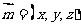 ,
,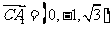 ,
,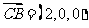 ,
,
所以
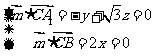 ,设
,设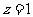 ,则
,则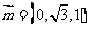 ,
,
故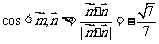 ,根据法向量的方向,
,根据法向量的方向,
可知二面角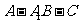 的余弦值大小为
的余弦值大小为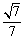
10. 22(空间向量)
9.(函数压轴题:)已知函数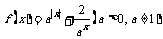 ,
,
(1)若 ,且关于
,且关于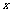 的方程
的方程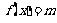 有两个不同的正数解,求实数
有两个不同的正数解,求实数 的取值范围;
的取值范围;
(2)记函数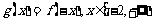 ,若
,若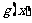 的最值与
的最值与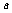 无关,求
无关,求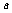 的取值范围.
的取值范围.
解:(1)令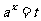 ,
,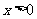 ,因为
,因为 ,所以
,所以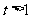 ,所以关于
,所以关于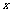 的方程
的方程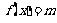 有两个不同的正数解等价于关于
有两个不同的正数解等价于关于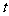 的方程
的方程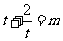 有相异的且均大于1的两根,即 关于
有相异的且均大于1的两根,即 关于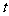 的方程
的方程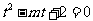 有相异的且均大于1的两根,
有相异的且均大于1的两根,
所以 ,
,
解得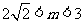 ,故实数
,故实数 的取值范围为区间
的取值范围为区间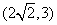 .
.
(2)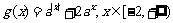
①当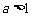 时,
时,
a)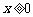 时,
时,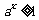 ,
,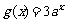 ,所以
,所以  ,
,
b)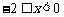 时,
时,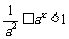
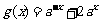 ,所以
,所以 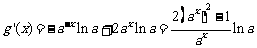
ⅰ当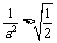 即
即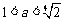 时,对
时,对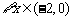 ,
,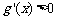 ,所以
,所以 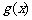 在
在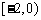 上递增,
上递增,
所以 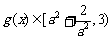 ,综合a) b)
,综合a) b)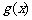 有最小值为
有最小值为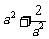 与a有关,不符合
与a有关,不符合
ⅱ当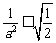 即
即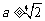 时,由
时,由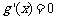 得
得 ,且当
,且当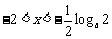 时,
时,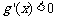 ,当
,当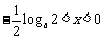 时,
时,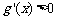 ,所以
,所以 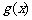 在
在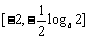 上递减,在
上递减,在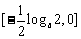 上递增,所以
上递增,所以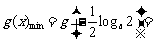
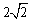 ,综合a) b)
,综合a) b)
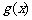 有最小值为
有最小值为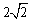 与a无关,符合要求.
与a无关,符合要求.
②当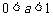 时,
时,
a) 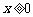 时,
时,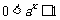 ,
,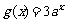 ,所以
,所以 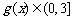
b) 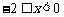 时,
时,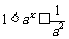 ,
,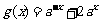 ,
,
所以 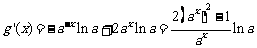
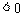 ,
,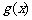 在
在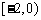 上递减,
上递减,
所以 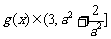 ,综合a) b)
,综合a) b)
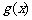 有最大值为
有最大值为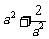 与a有关,不符合
与a有关,不符合
综上所述,实数a的取值范围是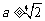 .
.
附加题22,23
8.(数列压轴题备选)已知数列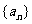 的通项公式是
的通项公式是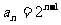 ,数列
,数列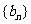 是等差数列,令集合
是等差数列,令集合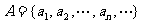 ,
,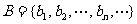 ,
,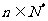 .将集合
.将集合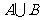 中的元素按从小到大的顺序排列构成的数列记为
中的元素按从小到大的顺序排列构成的数列记为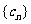 .
.
(1)若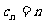 ,
,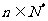 ,求数列
,求数列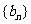 的通项公式; (2)若
的通项公式; (2)若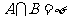 ,数列
,数列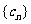 的前5项成等比数列,且
的前5项成等比数列,且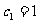 ,
,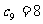 ,求满足
,求满足
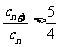 的正整数
的正整数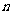 的个数.
的个数.
答案: (1) 或
或 或
或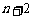
(2)分类讨论:数列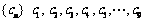
若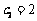 ;
;
 ;
;
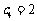 ;
;
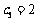 .
.
只有 满足,数列
满足,数列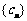 为1,
为1,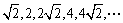 ,
,
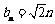 .
.
满足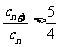 的
的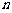 的值为1,2,3,4,6共5个.
的值为1,2,3,4,6共5个.
7.(数列压轴题)已知无穷数列{an}中,a1,a2,…,am是首项为10,公差为-2的等差数列;am+1,am+2,…,a2m是首项为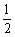 ,公比为
,公比为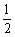 的等比数列(其中 m≥3,m∈N*),并对任意的n∈N*,均有an+2m=an成立.
的等比数列(其中 m≥3,m∈N*),并对任意的n∈N*,均有an+2m=an成立.
(1)当m=12时,求a2010;
(2)若a52=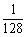 ,试求m的值;
,试求m的值;
(3)判断是否存在m(m≥3,m∈N*),使得S128m+3≥2010成立?若存在,试求出m的值;若不存在,请说明理由.
解(1)m=12时,数列的周期为24.
∵2010=24×83+18,而a18是等比数列中的项,
∴a2010=a18=a12+6=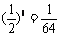 .
.
(2)设am+k是第一个周期中等比数列中的第k项,则am+k=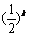 .
.
∵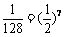 ,∴等比数列中至少有7项,即m≥7,则一个周期中至少有14项.
,∴等比数列中至少有7项,即m≥7,则一个周期中至少有14项.
∴a52最多是第三个周期中的项.
若a52是第一个周期中的项,则a52=am+7=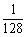 .
.
∴m=52-7=45;
若a52是第二个周期中的项,则a52=a3m+7=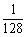 .∴3m=45,m=15;
.∴3m=45,m=15;
若a52是第三个周期中的项,则a52=a5m+7=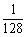 .∴5m=45,m=9;
.∴5m=45,m=9;
综上,m=45,或15,或9.
(3)2m是此数列的周期,
∴S128m+3表示64个周期及等差数列的前3项之和.
∴S2m最大时,S128m+3最大.
∵S2m=
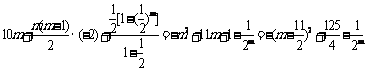 ,
,
当m=6时,S2m=31-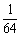 =
=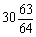 ;
;
当m≤5时,S2m<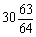 ;
;
当m≤7时,S2m< =29<
=29<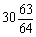 .
.
∴当m=6时,S2m取得最大值,则S128m+3取得最大值为64×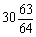 +24=2007.
+24=2007.
由此可知,不存在m(m≥3,m∈N*),使得S128m+3≥2010成立.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com