
22.(本题满分12分)
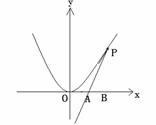 如图,已知直线
如图,已知直线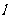 与抛物线
与抛物线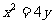 相切于点
相切于点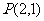 ,且与
,且与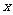 轴交于点
轴交于点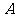 ,
,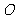 为坐标原点,定点
为坐标原点,定点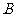 的坐标为
的坐标为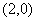
(1)若动点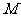 满足
满足 ,求点
,求点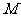 的轨迹
的轨迹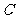 .
.
(2)若过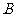 的直线
的直线 (斜率不等于0)与(1)中的轨迹
(斜率不等于0)与(1)中的轨迹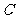 的交于不同的两点
的交于不同的两点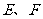 (
(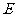 在
在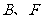 之间),试求
之间),试求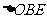 与
与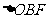 面积之比的取值范围。
面积之比的取值范围。
21.(本题满分12分)
设数列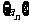 的前
的前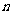 项和为
项和为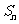 ,已知
,已知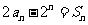 .
.
(1)求证: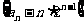 是等比数列.
是等比数列.
(2)求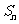 .
.
20.(本题满分12分)
函数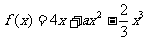 ,
,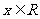 ,在区间[-1,1]上是增函数.
,在区间[-1,1]上是增函数.
(1)求实数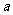 的取值组成的集合
的取值组成的集合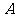 .
.
(2)设关于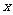 的方程
的方程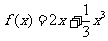 的两个非零实根为
的两个非零实根为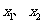 ,试问是否存在实数
,试问是否存在实数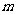 ,使得不等式
,使得不等式 对任意
对任意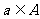 及
及 恒成立,若存在,求出
恒成立,若存在,求出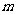 的取值范围,若不存在,说明理由.
的取值范围,若不存在,说明理由.
2.求某人方案2被录用的概率
1.求某人方案1被录用的概率;
19.(本题满分12分)
某公司计划通过考试招聘一些员工,考试课目有语文、数学、物理、化学、已知某人能通过语文、数学、物理、化学考试的概率分别是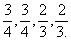 .现有两种方案
.现有两种方案
方案一:从语文、数学、物理、化学四门中随机抽取3门进行考试,3门都通过时才能录用.
方案二:四门都进行考试,其中有3门或3门以上通过时才能录用.
18.本题满分12分
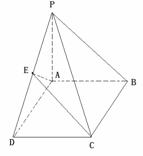 如图,在底面为平行四边形的四棱锥
如图,在底面为平行四边形的四棱锥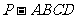 中,
中,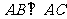 ,
,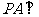 平面
平面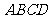 ,且
,且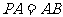 ,点
,点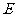 是
是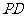 的中点.
的中点.
(1)求证: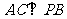
(2)求证: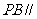 平面
平面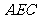
(3)求二面角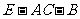 的大小
的大小
17.(本题满分10分)
在锐角 中,
中,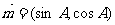
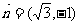
 。
。
(1)求角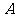 的大小
的大小
(2)求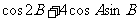 的取值范围
的取值范围
16.设直线系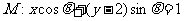
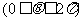 ,对于下列四个命题,
,对于下列四个命题,
(1)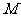 中所有直线均经过一个定点
中所有直线均经过一个定点
(2)存在定点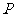 不在
不在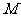 中的任一条直线上
中的任一条直线上
(3)对于任意整数 ,存在正
,存在正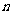 边形,其所有边均在
边形,其所有边均在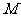 中的直
中的直
线上.
(4)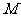 中的直线所围成的正三角形面积都相等.
中的直线所围成的正三角形面积都相等.
其中真命题的代号是 .(写出所有真命题代号)
15.等比数列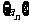 中,
中,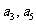 是一元二次方程
是一元二次方程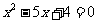 的根,则
的根,则
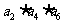 的值是
.
的值是
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com