
6.(2010年高考辽宁卷理科16)已知数列 满足
满足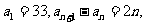 则
则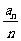 的最小值为_________
的最小值为_________ _.
_.
[答案]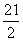
5.(2010年高考浙江卷15)设a1,d为实数,首项为a1,公差为d的等差数列{an }的前n项和为Sn,满足S5S6+15=0,则d的取值范围是 。
[答案] 或
或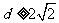
4.(2010年高考浙江卷14)设n≥ 2,n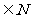 ,(2 x+
,(2 x+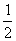 )
)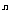 -(3x+
-(3x+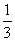 )
)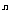 = a
= a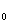 + a
+ a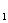 x2+…+ a
x2+…+ a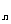 xn,将∣a
xn,将∣a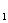 ∣(0≤k≤n)的最小值记为
∣(0≤k≤n)的最小值记为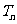 ,则
,则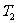 =0,
=0,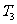 =
=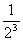 -
-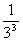 ,
,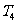 =0,
=0,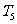 =
=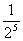 -
-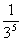 ,…
,…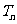 ,…
,…
其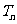 =_______.
=_______.
[答案]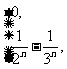
3.(2010年高考江苏卷试题8)函数y=x2(x>0)的图像在点(ak,ak2)处的切线与x轴交点的横坐标为ak+1,k为正整数,a1=16,则a1+a3+a5=____▲_____
[答案]21
[解析]考查函数的切线方程、数列的通项。
在点(ak,ak2)处的切线方程为: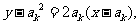 当
当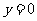 时,解得
时,解得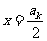 ,
,
所以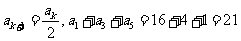 。
。
2. (2010年高考湖南卷理科15)若数列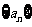 满足:对任意的
满足:对任意的 ,只有有限个正整数
,只有有限个正整数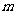 使得
使得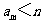 成立,记这样的
成立,记这样的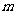 的个数为
的个数为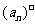 ,则得到一个新数列
,则得到一个新数列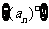 .例如,若数列
.例如,若数列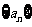 是
是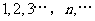 ,则数列
,则数列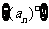 是
是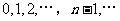 .已知对任意的
.已知对任意的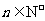 ,
,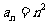 ,则
,则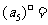 ,
,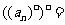
 .
.
[答案]2,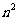
[解析]因为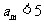 ,而
,而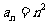 ,所以m=1,2,所以
,所以m=1,2,所以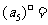 2.
2.
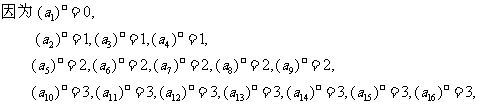
所以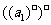 =1,
=1, 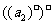 =4,
=4,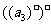 =9,
=9,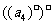 =16,
=16,
猜想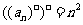
[命题意图]本题以数列为背景,通过新定义考察学生的自学能力、创新能力、探究能力,属难题。
1.(2010年高考福建卷理科11)在等比数列 中,若公比
中,若公比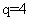 ,且前3项之和等于21,则该数列的通项公式
,且前3项之和等于21,则该数列的通项公式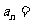 .
.
[答案]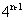
[解析]由题意知 ,解得
,解得 ,所以通项
,所以通项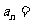
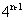 。
。
[命题意图]本题考查等比数列的通项公式与前n项和公式的应用,属基础题。
13. (2010年高考全国2卷理数4)如果等差数列
(2010年高考全国2卷理数4)如果等差数列 中,
中,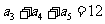 ,那么
,那么
(A)14 (B)21 (C)28 (D)35[答案]C
[命题意图]本试题主要考查等差数列的基本公式和性质.
[解析]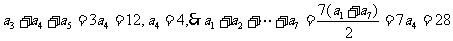
13(2010年高考重庆市理科1)在等比数列 中,
中,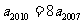 ,则公比q的值为
,则公比q的值为
(A) 2 (B) 3 (C) 4 (D) 8
[答案]A
解析: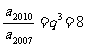
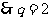 。
。
12.(2010年高考辽宁卷理科6)设{an}是有正数组成的等比数列, 为其前n项和。已知a2a4=1,
为其前n项和。已知a2a4=1, 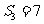 ,则
,则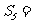
(A)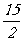 (B)
(B)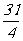 (C)
(C)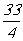 (D)
(D)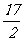
[答案]B
11.(2010年高考浙江卷3)设Sn 为等比数列{an}的前n项和,8a2+ a5=0, 则S5/S2=
(A)11 (B)5 (C)-8 (D)-11
[答案]D
10.(2010年高考江西卷理科5)等比数列 中,
中,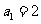 ,
,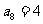 ,函数
,函数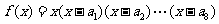 ,则
,则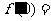
A.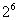 B.
B.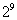 C.
C.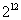 D.
D.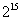
[答案]C
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com