
8.动点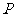 到点
到点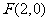 的距离与它到直线
的距离与它到直线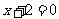 的距离相等,则
的距离相等,则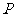 的轨迹方程为 。
的轨迹方程为 。
7.圆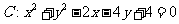 的圆心到直线
的圆心到直线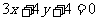 的距离
的距离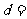 。
。
6.已知四棱椎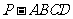 的底面是边长为6 的正方形,侧棱
的底面是边长为6 的正方形,侧棱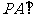 底面
底面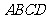 ,且
,且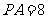 ,
,
则该四棱椎的体积是 。
5.将一个总数为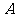 、
、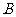 、
、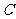 三
三 层,其个体数之比为5:3:2。若用分层抽样方法抽取容量为100的样本,则应从
层,其个体数之比为5:3:2。若用分层抽样方法抽取容量为100的样本,则应从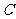 中抽取
个个体。
中抽取
个个体。
4.若复数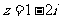 (
(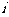 为虚数单位),则
为虚数单位),则 。
。
3.行列式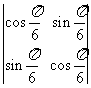 的值是
。
的值是
。
2.不等式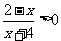 的解集是
。
的解集是
。
1.已知集合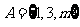 ,
,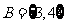 ,
,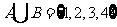 则
则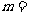 。
。
(17)(本小题满分12分)
设等差数列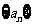 满足
满足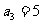 ,
,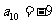 。
。
(Ⅰ)求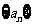 的通项公式;
的通项公式;
(Ⅱ)求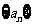 的前
的前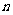 项和
项和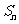 及使得
及使得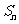 最大的序号
最大的序号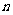 的值。
的值。
(18)(本小题满分12分)
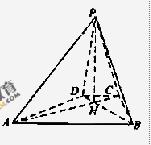
如图,已知四棱锥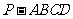 的底面为等腰梯形,
的底面为等腰梯形,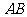 ∥
∥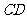 ,
,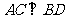 ,垂足为
,垂足为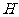 ,
,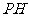 是四棱锥的高。
是四棱锥的高。
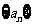
(Ⅰ)证明:平面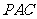
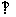 平面
平面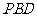 ;
;
(Ⅱ)若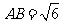 ,
,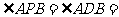 60°,求四棱锥
60°,求四棱锥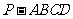 的体积。
的体积。
请考生在第(22)、(23)、(24)三题中任选一题作答,如果多做,则按所做的第一题计分。作答时用2B铅笔在答题卡上把所选题目的题号涂黑。
(19)(本小题满分12分)
为调查某地区老年人是否需要志愿者提供帮助,用简单随机抽样方法从该地区调查了500位老人,结果如下:

(Ⅰ)估计该地区老年人中,需要志愿提供帮助的老年人的比例;
(Ⅱ)能否有99℅的把握认为该地区的老年人是否需要志愿者提供帮助与性别有关?
(Ⅲ)根据(Ⅱ)的结论,能否提出更好的调查办法来估计该地区的老年人中,需要志愿者提供帮助的老年人的比例?说明理由。
附:

(20)(本小题满分12分)
设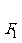 ,
,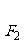 分别是椭圆E:
分别是椭圆E: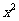 +
+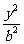 =1(0﹤b﹤1)的左、右焦点,过
=1(0﹤b﹤1)的左、右焦点,过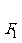 的直线
的直线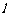 与E相交于A、B两点,且
与E相交于A、B两点,且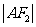 ,
,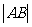 ,
,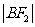 成等差数列。
成等差数列。
(Ⅰ)求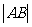
(Ⅱ)若直线 的斜率为1,求b的值。
的斜率为1,求b的值。
(21)本小题满分12分)
设函数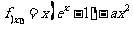
(Ⅰ)若a=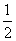 ,求
,求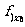 的单调区间;
的单调区间;
(Ⅱ)若当 ≥0时
≥0时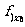 ≥0,求a的取值范围
≥0,求a的取值范围
(22)(本小题满分10分)选修4-1:几何证明选讲
如图:已知圆上的弧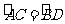 ,过C点的圆的切线与BA的延长线交于
,过C点的圆的切线与BA的延长线交于
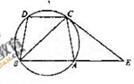 E点,证明:
E点,证明:
(Ⅰ)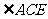 =
=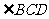 。
。
(Ⅱ)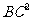 =BE x CD。
=BE x CD。
(23)(本小题满分10分)选修4-4:坐标系与参数方程
|
|
|
|
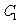 :{ {t为参数}。图
:{ {t为参数}。图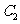 :{ {
:{ {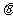 为参数}
为参数}
(Ⅰ)当a=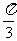 时,求
时,求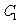 与
与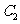 的交点坐标:
的交点坐标:
(Ⅱ)过坐标原点O做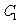 的垂线,垂足为A、P为OA的中点,当a变化时,
的垂线,垂足为A、P为OA的中点,当a变化时,

求P点轨迹的参数方程,并指出它是什么曲线。
(24)(本小题满分10分)选修4-5:不等式选讲
设函数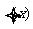 =
=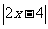 + 1。
+ 1。
(Ⅰ)画出函数y=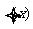 的图像:
的图像:
(Ⅱ)若不等式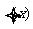 ≤ax的解集非空,求n的取值范围
≤ax的解集非空,求n的取值范围
(1)已知集合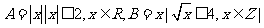 ,则
,则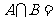
(A)(0,2) (B)[0,2] (C)|0,2| (D)|0,1,2|
(2)a,b为平面向量,已知a=(4,3),2a+b=(3,18),则a,b夹角的余弦值等于
(A)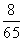 (B)
(B)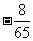 (C)
(C)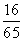 (D)
(D)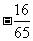
(3)已知复数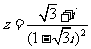 ,则
,则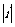 =
=
(A)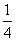 (B)
(B)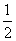 (C)1
(D)2
(C)1
(D)2
(4)曲线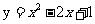 在点(1,0)处的切线方程为
在点(1,0)处的切线方程为
(A)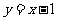 (B)
(B)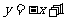
(C)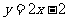 (D)
(D)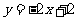
(5)中心在远点,焦点在 轴上的双曲线的一条渐近线经过点(4,2),则它的离心率为
轴上的双曲线的一条渐近线经过点(4,2),则它的离心率为
(A)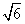 (B)
(B)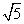
(C) (D)
(D)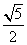
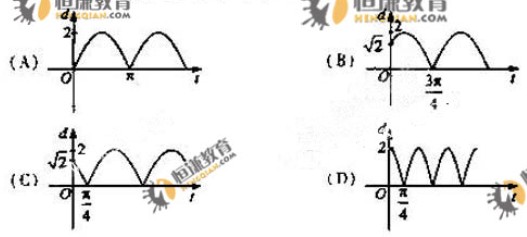
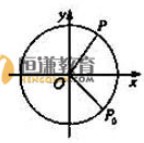 (6)如图,质点
(6)如图,质点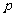 在半径为2的圆周上逆时针运动,其初始位置为
在半径为2的圆周上逆时针运动,其初始位置为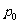 (
(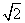 ,
, ),角速度为1,那么点
),角速度为1,那么点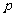 到
到 轴距离
轴距离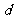 关于时间
关于时间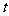 的函数图像大致为
的函数图像大致为
(7) 设长方体的长、宽、高分别为2a、a、a,其顶点都在一个球面上,则该球的表面积为
(A)3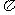 a2
(B)6
a2
(B)6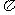 a2
(C)12
a2
(C)12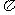 a2
(D) 24
a2
(D) 24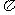 a2
a2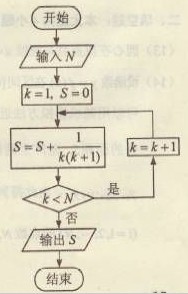 (8)如果执行右面的框图,输入N=5,则输出的数等于
(8)如果执行右面的框图,输入N=5,则输出的数等于
(A)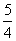
(B)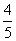
(C)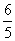
(D)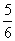
(9)设偶函数f(x)满足f(x)=2x-4 (x 0),则
0),则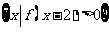 =
=
(A) (B)
(B)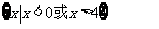
(C)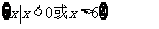 (D)
(D)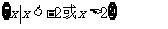
(10)若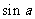 = -
= -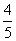 ,a是第一象限的角,则
,a是第一象限的角,则
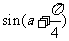 =
=
(A)-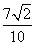 (B)
(B)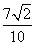 (C)
(C)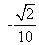 (D)
(D)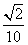
(11)已知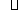 ABCD的三个顶点为A(-1,2),B(3,4),C(4,-2),点(x,y)在
ABCD的三个顶点为A(-1,2),B(3,4),C(4,-2),点(x,y)在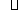 ABCD的内部,则z=2x-5y的取值范围是
ABCD的内部,则z=2x-5y的取值范围是
(A)(-14,16) (B)(-14,20) (C)(-12,18) (D)(-12,20)
(12)已知函数f(x)=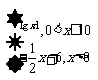 若a,b,c均不相等,且f(a)= f(b)= f(c),则abc的取值范围是
若a,b,c均不相等,且f(a)= f(b)= f(c),则abc的取值范围是
(A)(1,10) (B)(5,6) (C)(10,12) (D)(20,24)
第Ⅱ卷
本卷包括必考题和选考题两部分。第(13)题~第(21)题为必考题,每个试题考生都必须做答。第(22)题~第(24)题为选考题,考生根据要求做答。
二填空题:本大题共4小题,每小题5分。
(13)圆心在原点上与直线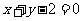 相切的圆的方程为-----------。
相切的圆的方程为-----------。
(14)设函数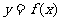 为区间
为区间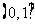 上的图像是连续不断的一条曲线,且恒有
上的图像是连续不断的一条曲线,且恒有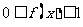 ,可以用随机模拟方法计算由曲线
,可以用随机模拟方法计算由曲线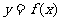 及直线
及直线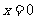 ,
,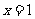 ,
,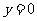 所围成部分的面积,先产生两组
所围成部分的面积,先产生两组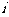 每组
每组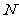 个,区间
个,区间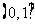 上的均匀随机数
上的均匀随机数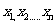 和
和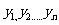 ,由此得到V个点
,由此得到V个点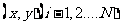 。再数出其中满足
。再数出其中满足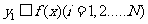 的点数
的点数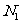 ,那么由随机模拟方法可得S的近似值为___________
,那么由随机模拟方法可得S的近似值为___________
(15)一个几何体的正视图为一个三角形,则这个几何体可能是下列几何体中的_______(填入所有可能的几何体前的编号)
①三棱锥 ②四棱锥 ③三棱柱 ④四棱柱 ⑤圆锥 ⑥圆柱
(16)在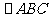 中,D为BC边上一点,
中,D为BC边上一点,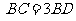 ,
,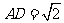 ,
,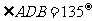 .若
.若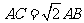 ,则BD=_____
,则BD=_____
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com