
(17)(本小题满分12分)
已知函数f(x)=sin(π -ωx) cosωx. cos2 ωx(ωx>0)的最小正周期为π 。
(Ⅰ)求的值.
( Ⅱ )将函数y=f(x)的图像上各点的横坐标缩短到原来的1/2,从坐标不变,得到函数y=f(x)的图像,求函数g(x)在区间[0, π /16] 上的最小值。
(18)(本小题满分12分)
已知等差数列{an}满足:a3=7,a5+a7=26.{an}的前n 项和为Sn..
(Ⅰ)求an及Sn ;
(Ⅱ)令bn= 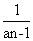 (n
(n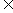 N+),求数列{an}的前n项和Tn。
N+),求数列{an}的前n项和Tn。
(19)(本小题满分12分)
一个袋中装有四个形状大小完全相同的球,球的编号分别为1,2,3,4,
(Ⅰ)从袋中随机取出两个球,求取出的球的编号之和不大于4的概率;
(Ⅱ)先从袋中随机取一个球,该球的编号为m,将球放回袋中,然后再从袋中随机取一个球,该球的编号为n,求n<m+2的概率。
(20)(本小题满分12分)
在如图所示的几何体中,四边形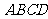 是正方形,
是正方形,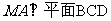 ,
,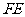 //
//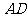 ,
,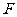 分别为
分别为
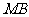 、
、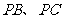 的中点,且
的中点,且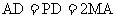 .
.
(Ⅰ) 求证:平面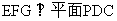 ;
;
(Ⅱ)求三棱锥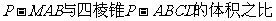
(21)(本小题满分12分)
已知函数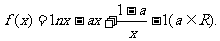
(Ⅰ)当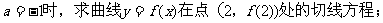
(Ⅱ)当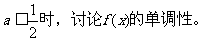
(22)(本小题满分14分)
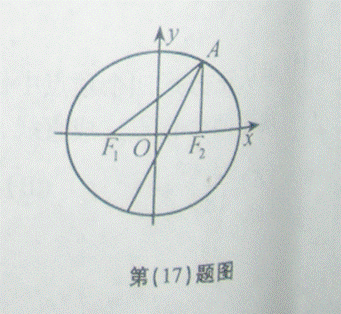
如图,已知椭圆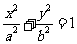 (a>b>0)过点(1,
(a>b>0)过点(1,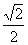 ),离心率为
),离心率为 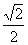 ,左右焦点分别为F1,F2.点P为直线L:x+y=2上且不在x轴上的任意一点,直线PF1和PF2与椭圆的交点分别为A、B和C、D。
,左右焦点分别为F1,F2.点P为直线L:x+y=2上且不在x轴上的任意一点,直线PF1和PF2与椭圆的交点分别为A、B和C、D。
O为坐标原点。
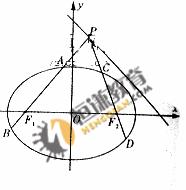
(Ⅰ) 求椭圆的标准方程;
(Ⅱ)设直线PF1、PF2斜率分别为k1、k2.
(ⅰ) 证明:1/k1-3/k3=2;
(ⅱ )问直线上是否存在一点,使直线OA、OB、OC、OD的斜率kOA, kOB, kOC, kOD满足kOA+k OB+kOC+kOD=0?若存在,求出所有满足条件的点P的坐标;若不存在,说明理由。
2010普通高等学校招生全国统一考试(山东卷)
(1) 已知全集U=R,集合M={x/x2-4≤0},则CuM=
(A){x/-2<x<2} (B){x/-2≤x≤2}
(C){x/x<-2或x>2} (D) {x/≤-2或x≥2}
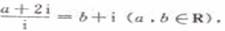
(2) 已知
其中i为虚数单位,则a+b=
(A)-1 (B)1 (C)2 (D)
(3)
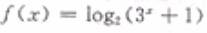 的值域为
的值域为
(A)(0,+∞) (B)[0,+∞] (C)(0,+∞) (D)[1,+∞(4)在空间,下列命题正确的是
(A)平行直线的平行投影重合 (B)平行于同一直线的两个平面
(C)垂直于同一平面的两个平面平行 (D)垂直于同一平面的两个平面平行
(5)设f(x)为定义在R上的函数。当x≥ 0时,f(x)=2x+2x+b (b为常数),则f(-1)=
(A). -3 (B). -1 (C). 1 (D). 3
(6 )在某项体育比赛中一位同学被评委所打出的分数如下:
90 89 90 90 94 93
去掉一个最高分和一个最低分后,所剩数据的平均分值为和方差分别为
(A) 92,2 (B) 92 ,2.8
(C)93,2 (D)93,2.8
(7)设{an}是首项大于岭南的等比数列,则“a1<a2”是数列{an},是递增数列的
(A)充分而不必要条件 (B)必要而不充分条件
(C)充分而不必要条件 (D)既不充分也不必要条件
(8)已知某生产厂家的年利润y(单位:万元)与年产量x(单位:万件)的函数关系式为y=-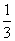 x3+81x-234,则该生产厂家获取最大年利润的年产量为
x3+81x-234,则该生产厂家获取最大年利润的年产量为
(A)13万件 (B)11万件 (C)9万件 (D)7万件
(9)已知抛物线y2=2px(p>0),过其交点且斜率为1的直线交抛物线于A、B两点,若线段AB的中点的纵坐标为2,则该抛物线的标准方程为
(A)x=1 (B)x=-1(
(C)x=2 (D)x=-2
(10)观察(x2)’=2x,(x4)’=4x3,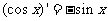 ,又归纳推理可得:若定义在R上的函数f(x)满足f(-x)= f(x),记g(x)为f(x)的导函数,则g(-x)=
,又归纳推理可得:若定义在R上的函数f(x)满足f(-x)= f(x),记g(x)为f(x)的导函数,则g(-x)=
(A)f(x) (B)-f(x) (C)g(x) (D)-g(x)
(11)函数y=2x-x2的图像大致是

(A) (B) (C) (D)
(12)定义平面向量之间的一种运算“⊙”如下:对任意的a=(m,n),b=(p,q),令a⊙b=mq-np.下面说法错误的是
(A)若a与b共线,则a⊙b=0
(B)a⊙b=b⊙a
(C)对任意的λ ∈R,有(λa)⊙b=λ(a⊙b)
(D)(a⊙b)2+(a·b)2=|a|2|b|2
第 卷(共90分)
卷(共90分)
二 填空题:本大题共4小题,每小题4分,共16分
(13)执行右图所示流程框图,若输入 x=4,则输出y的值为____________________.
(14) 已知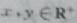 ,且满足
,且满足 ,则xy的最
,则xy的最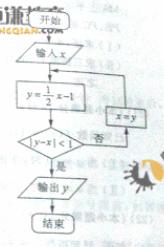 大值为____________________.
大值为____________________.
(15)在 中,角A、B、C所对的边分别为a、b、c。若
中,角A、B、C所对的边分别为a、b、c。若 ,则角A的大小为____________________.
,则角A的大小为____________________.
(16) 已知圆C过点(1,0),且圆心在x轴的正半轴上,直线 被该圆所截得的弦长为
被该圆所截得的弦长为 ,则圆C的标准方程为____________
,则圆C的标准方程为____________
(16)△ABC的面积是30,内角A,B,C,所对边长分别为a,b,c,cosA=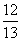 .
.
(1)求
(2)若c-b= 1,求a的值.
1,求a的值.
(17)椭圆E经过点A(2,3),对称轴为坐标轴,焦点F1,F2在x轴上,离心率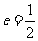 .
.
(1)求椭圆E的方程;
(2)求∠F1AF2的角平分线所在直线的方程.
18、(本小题满分13分)
某市20104月1日-4月30日对空气 污染指数的检测数据如下(主要污染物为可吸入颗粒物):
污染指数的检测数据如下(主要污染物为可吸入颗粒物):
61,76,70,56,81,91,92,91,75 ,81,88,67,101,103,95,91,
,81,88,67,101,103,95,91,
77,86,81,83,82,82,64,79,86,85,75,71,49,45,
(Ⅰ) 完成频率分布表;
(Ⅱ)作出频率分布直方图;
(Ⅲ)根据国家标准,污 染指数在0~50之间时
染指数在0~50之间时 ,空气质量为优:在51~100之间时,为良;在101~150之间时,为轻微污染;在151~200之间时,为轻度污染。
,空气质量为优:在51~100之间时,为良;在101~150之间时,为轻微污染;在151~200之间时,为轻度污染。
请你依据所给数据和上述标准,对 该市的空气质量给出一个简短评价.
该市的空气质量给出一个简短评价.
(19) (本小题满分13分)
如图,在多面体ABCDEF中,四边形ABCD是正方形,AB=2EF=2,E F∥AB,EF⊥FB,∠BFC=90°,BF=FC,H为BC的中点,
F∥AB,EF⊥FB,∠BFC=90°,BF=FC,H为BC的中点,
(Ⅰ)求证:FH∥平面EDB;
(Ⅱ)求证:AC⊥平面EDB;
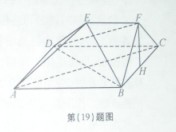
(Ⅲ)求四面体B-DEF的体积;
(20)(本小题满分12分)
设函数f(x)= sinx-cosx+x+1, 0﹤x﹤2∏,求函数f(x)的单调区间与极值.
sinx-cosx+x+1, 0﹤x﹤2∏,求函数f(x)的单调区间与极值.
(21)(本小题满分13分)
设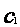 ,
,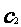 ...,
...,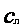 ,…是坐标平面上的一列圆,它们的圆心都在x轴的正半轴上,且都与直线y=
,…是坐标平面上的一列圆,它们的圆心都在x轴的正半轴上,且都与直线y=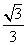 x相切,对每一个正整数n,圆
x相切,对每一个正整数n,圆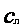 都与圆
都与圆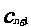 相互外切,以
相互外切,以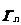 表示
表示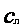 的半径,已知
的半径,已知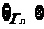 为递增数列.
为递增数列.
(Ⅰ)证明: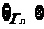 为等比数列;
为等比数列;
(Ⅱ)设 =1,求数列
=1,求数列 的前n项和.
的前n项和. 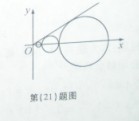
(11)命题“存在x∈R,使得x2+2x+5=0”的否定是
(12)抛物线y2=8x的焦点坐标是
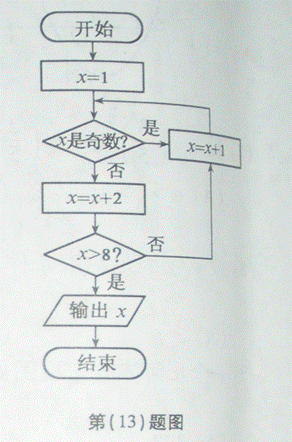
(13)如图所示,程序框图(算法流程图)的输出值x=
(14)某地有居民100000户,其中普通家庭99 000户,高收入家庭1 000户.从普通家庭中以简单随机抽样方式抽取990户,从高收入家庭中以简单随机抽样方式抽取l00户进行调查,发现共有120户家庭拥有3套或3套以上住房,其中普通家庭50户,高收人家庭70户.依据这些数据并结合所掌握的统计知识,你认为该地拥有3套或3套以上住房的家庭所占比例的合理估计是 .
(15)若a>0 ,b>0,a+b=2,则下列不等式对一切满足条件的a.
,b>0,a+b=2,则下列不等式对一切满足条件的a.
b恒成立的是 (写出所有正确命题的编号).
①ab≤1; ②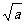 +
+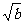 ≤
≤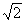 ; ③a2+b2≥2;
; ③a2+b2≥2;
④a3+b3≥3; 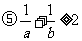
(1)若A=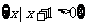 ,B=
,B=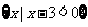 ,则
,则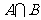 =
=
(A)(-1,+∞) (B)(-∞,3) (C)(-1,3) (D)(1,3)
(2)已知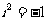 ,则i(
,则i(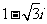 )=
)=
(A)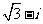 (B)
(B)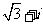 (C)
(C)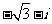 (D)
(D)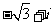
(3)设向量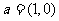 ,
,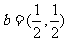 ,则下列结论中正确的是
,则下列结论中正确的是
(A)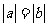 (B)
(B)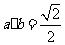
(C)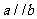
 (D)
(D) 与
与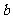 垂直
垂直
(4)过 点(1,0)且与直线x-2y-2=0平行的直线方程是
点(1,0)且与直线x-2y-2=0平行的直线方程是
(A)x-2y-1=0 (B)x-2y+1=0
(C)2x+y-2=0 (D)x+2y-1=0
(5)设数列{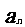 }的前n项和
}的前n项和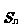 =
=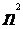 ,则
,则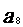 的值为
的值为
(A) 15 (B) 16 (C) 49 (D)64
(6)设abc>0,二次函数f(x)=a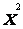 +bx+c的图像可能是
+bx+c的图像可能是

(7)设a= ,b=
,b=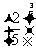 ,c=
,c=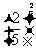 ,则a,b,c的大小关系是
,则a,b,c的大小关系是
(A)a>c>b (B)a>b>c (C)c>a>b (D)b>c>a
(8)设x,y满足约束条件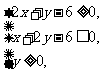 则目标
则目标 函数z=x+y的最大值是
函数z=x+y的最大值是
(A)3 (B) 4 (C) 6 (D)8
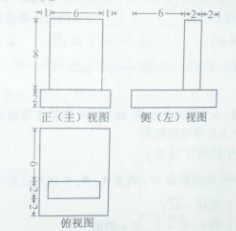
(9)一个几何体的三视图如图,该几何体的表面积是
(A)372 (C)292
(B)360 (D)280

(10)甲从正方形四个顶点中任意选择两个顶点连成直线,一页从该正方形四个顶点中任意选择连个顶点连成直线,则所得的两条直线相互垂直的概率是
(A)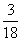
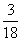 (A)
(A)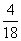 (A)
(A)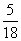
 (A)
(A)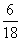
数 学(文科)(安徽卷)
第Ⅱ卷(非选择题共100分)
请用0 5毫米黑色墨水签字笔在答题卡上作答,在试题卷上大体无效。
(17)(本小题满分12分)
在△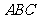 中,
中,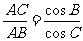 。
。
(Ⅰ)证明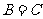 :
:
(Ⅱ)若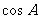 =
=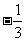 ,求
,求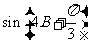 的值。
的值。
(18)(本小题满分12分)
有编号为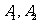 ,…,
,…,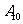 的10个零件,测量其直径(单位:cm),得到下面数据:
的10个零件,测量其直径(单位:cm),得到下面数据:
|
编号 |
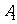 |
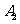 |
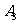 |
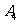 |
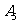 |
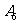 |
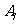 |
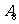 |
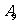 |
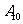 |
|
直径 |
1.51 |
1.49 |
1.49 |
1.51 |
1.49 |
1.51 |
1.47 |
1.46 |
1.53 |
1.47 |
其中直径在区间[1.48,1.52]内的零件为一等品。
(Ⅰ)从上述10个零件中,随机抽取一个,求这个零件为一等品的概率:
(Ⅱ)从一等品零件中,随机抽取2个。
(i)用零件的编号列出所有可能的抽取结果;
(ii)求这2个零件直径相等的概率。
(19)(本小题满分12分)
 如图,在五面体
如图,在五面体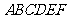 中,四边形
中,四边形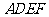 是正方形,
是正方形,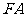 ⊥平面
⊥平面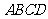 ,
,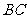 ∥
∥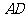 ,
,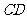 =1,
=1,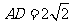 ,∠
,∠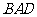 =∠
=∠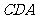 =45°。
=45°。
(Ⅰ)求异面直线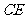 与
与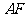 所成角的余弦值;
所成角的余弦值;
(Ⅱ)证明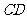 ⊥平面
⊥平面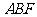 ;
;
(Ⅲ)求二面角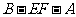 的正切值。
的正切值。
(20)(本小题满分12分)
已知已知函数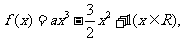 其中
其中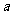 >0。
>0。
(Ⅰ)若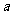 =1,求曲线
=1,求曲线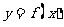 在点(2,
在点(2,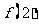 )处的切线方程:
)处的切线方程:
(Ⅱ)若在区间 上,
上,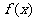 >0恒成立,求
>0恒成立,求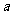 的取值范围。
的取值范围。
(21)(本小题满分14分)
已知椭圆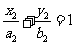 (a>b>0)的离心率e=
(a>b>0)的离心率e=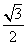 ,连接椭圆的四个顶点得到的菱形的面积为4。
,连接椭圆的四个顶点得到的菱形的面积为4。
(Ⅰ)求椭圆的方程
(Ⅱ)设直线l与椭圆相交于不同的两点A,B,已知点A的坐标为(-a,0).
(i)
若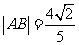 ,求直线l的倾斜角;
,求直线l的倾斜角;
(ii)
若点Q(0,yo)在线段AB的垂直平分线上,且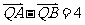 ,求yo的值。
,求yo的值。
(22)(本小题满分14分)
在数列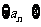 中,a1=0,且对任意
中,a1=0,且对任意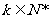 ,
,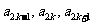 成等差数列,其公差为2k。
成等差数列,其公差为2k。
(Ⅰ)证明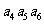 成等比数列;
成等比数列;
(Ⅱ)求数列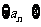 的通项公式;
的通项公式;
(Ⅲ)记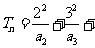 ……+
……+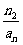 ,证明
,证明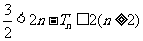
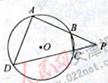 (11)如图,四边形ABCD是圆O的内接四边形,延长AB和DC相交于点P。若PB=1,PD=3,则
(11)如图,四边形ABCD是圆O的内接四边形,延长AB和DC相交于点P。若PB=1,PD=3,则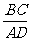 的值为
。
的值为
。
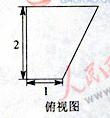
12.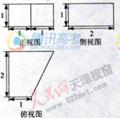 一个几何体的三视图如图所示,则这个几何体的体积为
。
一个几何体的三视图如图所示,则这个几何体的体积为
。
(13)已知双曲线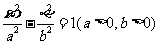 的一条渐近线方程是
的一条渐近线方程是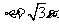 ,它的一个焦点与抛物线
,它的一个焦点与抛物线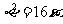 的焦点相同,则双曲线的方程为
。
的焦点相同,则双曲线的方程为
。
(14)已知圆C的圆心是直线 与
与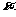 轴的交点,且圆C与直线
轴的交点,且圆C与直线 相切。则圆C的方程为
。
相切。则圆C的方程为
。
(15)设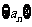 是等比数列,公比
是等比数列,公比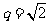 ,
,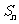 为
为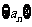 的前
的前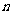 项和,记
项和,记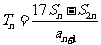 ,
,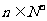 .设
.设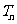 为数列
为数列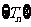 的最大项,则
的最大项,则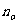 =
.
=
.
(16)设函数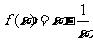 ,对任意
,对任意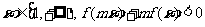 恒成立,则实数m的取值范围是
.
恒成立,则实数m的取值范围是
.
⒂(共13 分)
分)
解:(Ⅰ)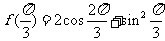 =
=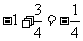
(Ⅱ)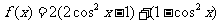
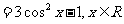
因为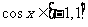 ,所以,当
,所以,当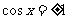 时
时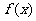 取最大值2;当
取最大值2;当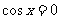 时,
时,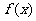 去最小值-1。
去最小值-1。
⒃(共13分)
解:(Ⅰ)设等差数列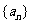 的公差
的公差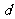 。
。
因为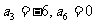
所以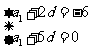 解得
解得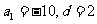
所以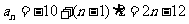
(Ⅱ)设等比数列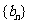 的公比为
的公比为
因为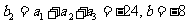
所以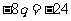 即
即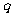 =3
=3
所以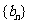 的前
的前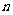 项和公式为
项和公式为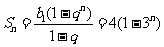
⒄(共13分)
证明:(Ⅰ)设AC于BD交于点G。因为EF∥AG,且EF=1,AG=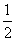 AG=1
AG=1
所以四边形AGE F为平行四边形
F为平行四边形
所以AF∥EG
因为EG 平面BDE,AF
平面BDE,AF 平面BDE,
平面BDE,
所以AF∥平面BDE
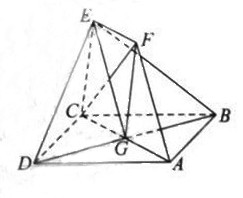
(Ⅱ)连接FG。因为EF∥CG,EF=CG=1,且CE=1,所以平行四边形CE FG为菱形。所以CF⊥EG.
FG为菱形。所以CF⊥EG.
 因为四边形ABCD为正方形,所以BD⊥AC.又因为平面ACEF⊥平面ABCD,且平面ACEF∩平面ABCD=AC,所以BD⊥平面ACEF.所以CF⊥BD.又BD∩EG=G,所以CF⊥平面BDE.
因为四边形ABCD为正方形,所以BD⊥AC.又因为平面ACEF⊥平面ABCD,且平面ACEF∩平面ABCD=AC,所以BD⊥平面ACEF.所以CF⊥BD.又BD∩EG=G,所以CF⊥平面BDE.
(18)(共14分)
解:由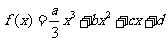 得
得 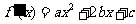
因为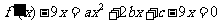 的两个根分别为1,4,所以
的两个根分别为1,4,所以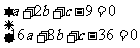 (*)
(*)
(Ⅰ)当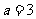 时,又由(*)式得
时,又由(*)式得
 解得
解得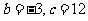
又因为曲线 过原点,所以
过原点,所以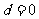
故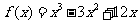
(Ⅱ)由于a>0,所以“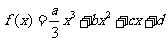 在(-∞,+∞)内无极值点”等价于“
在(-∞,+∞)内无极值点”等价于“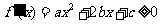 在(-∞,+∞)内恒成立”。
在(-∞,+∞)内恒成立”。
由(*)式得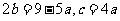 。
。
又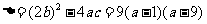
解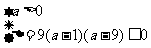 得
得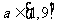
即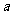 的取值
的取值 范围
范围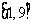
(19)(共14分)
解:(Ⅰ)因为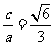 ,且
,且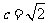 ,所以
,所以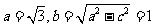
所以椭圆C的方程为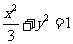
(Ⅱ)由题意知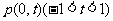
由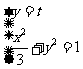 得
得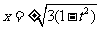
所以圆P的半径为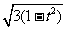
解得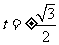 所以点P的坐标是(0,
所以点P的坐标是(0,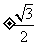 )
)
(Ⅲ)由(Ⅱ)知,圆P的方程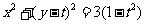 。因为点
。因为点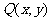 在
在 圆P上。所以
圆P上。所以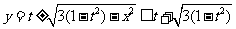
设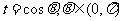 ,则
,则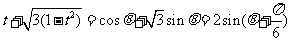
当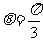 ,即
,即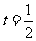 ,且
,且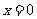 ,
,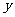 取最大值2.
取最大值2.
(20)(共13分)
(Ⅰ)解: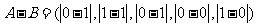 =(1,0,1,0,1)
=(1,0,1,0,1)
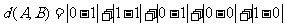 =3
=3
(Ⅱ)证明:设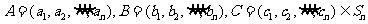
因为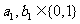 ,所以
,所以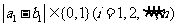
从而
由题意知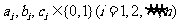
当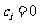 时,
时,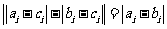
当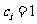 时
时 ,
,
所以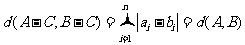
(Ⅲ)证明:设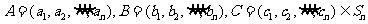
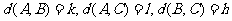
记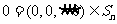 由(Ⅱ)可知
由(Ⅱ)可知
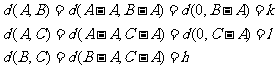
所以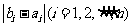 中1的个数为k,
中1的个数为k,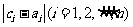 中1的个数为
中1的个数为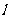
设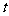 是使
是使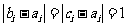 成立的
成立的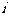 的个数。则
的个数。则
由此可知,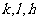 三个数不可能都是奇数
三个数不可能都是奇数
即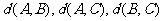 三个数中至少有一个是偶数。
三个数中至少有一个是偶数。
⑼ 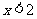
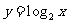 ⑽ 1
⑽ 1
⑾ -3
⑿ 0.030 3
⒀ (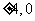 )
) 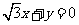 ⒁ 4
⒁ 4 
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com