
4、某棉纺厂为了了解一批棉花的质量,从中随机抽取了100根棉花纤维的长度(棉花纤维的长度是棉花质量的重要指标),所得数据都在区间[5,40]中,其频率分布直方图如图所示,则其抽样的100根中,有_▲___根在棉花纤维的长度小于20mm。
答案:30
3、盒子中有大小相同的3只小球,1只黑球,若从中随机地摸出两只球,两只球颜色不同的概率是_▲__
答案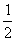
2、设复数z满足z(2-3i)=6+4i(其中i为虚数单位),则z的模为______▲________
答案: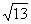
1、设集合A={-1,1,3},B={a+2,a2+4},A∩B={3},则实数a=______▲________
答案:1
(17)(本小题满分10 分)(注意:在试题卷上作答无效)
分)(注意:在试题卷上作答无效)
记等差数列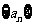 的前
的前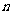 的和为
的和为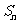 ,设
,设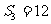 ,且
,且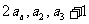 成等比数列,求
成等比数列,求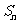 .
.
(18)(本小题满分12分)(注意:在试题卷上作答 无效)
无效)
已知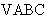 的内角
的内角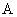 ,
,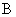 及其对边
及其对边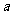 ,
,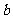 满足
满足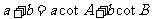 ,求内角
,求内角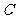 .
.
(19)(本小题满分12分)(注意:在试题卷上作答无效)
投到某杂志的稿件,先由两位初审专家进行评审.若能通过两位初审专家的评审,
则予以录用;若两位初审专家都未予通过,则不予录用;若恰能通过一位初审专家的评
审,则再由 第三位专家进行复审,若能通过复审专家的评审,则予以录用,否则不予录
第三位专家进行复审,若能通过复审专家的评审,则予以录用,否则不予录
用.设稿件能通过各初审专家评审的概率均为0.5,复审的稿件能通过评审的概率为0.3.
各专家独立评审.
(I)求投到该杂志的1篇稿件被录用的概率;
(II)求投到该杂志的4篇稿件中,至少有2篇被录用的概率.
(20)(本小题满分12分)(注意:在试题卷上作答无效)
如图,四棱锥S-ABCD中,SD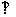 底面ABCD,AB//DC,AD
底面ABCD,AB//DC,AD DC,AB=AD=1,DC=SD=2,E为棱SB上的一点,平面EDC
DC,AB=AD=1,DC=SD=2,E为棱SB上的一点,平面EDC 平面SBC .
平面SBC .
(Ⅰ)证明:SE=2EB;
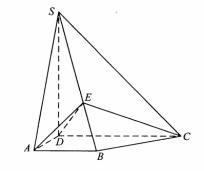 (Ⅱ)求二面角A-DE-C的大小 .
(Ⅱ)求二面角A-DE-C的大小 .
(21)(本小题满分1 2分)(注意:在试题卷上作答无效)
2分)(注意:在试题卷上作答无效)
已知函数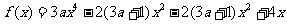
(I)当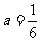 时,求
时,求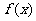 的极值;
的极值;
(II)若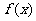 在
在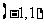 上是增函数,求
上是增函数,求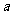 的取值范围
的取值范围
(22)(本小题满分12分)(注意:在试题卷上作答无效)
已知抛物线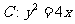 的焦点为F,过点
的焦点为F,过点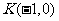 的直线
的直线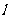 与
与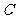 相交于
相交于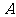 、
、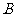 两点,点A关于
两点,点A关于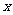 轴的对称点为D .
轴的对称点为D .
(Ⅰ)证明:点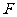 在直线
在直线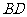 上;
上;
(Ⅱ)设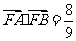 ,求
,求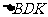 的内切圆
的内切圆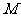 的方程 .
的方程 .
(注意:在试题卷上作答无效)
(13)不等式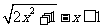 的解集是
.
的解集是
.
(14)已知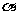 为第三象限的角,
为第三象限的角,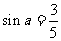 ,则
,则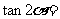 .
.
(15)某学校开设A类选修课3门,B类选修课4门,一位同学从中共选3门 ,若要求两类课程各自少选一门,则不同的选法共有
种.(用数字作答)
,若要求两类课程各自少选一门,则不同的选法共有
种.(用数字作答)
(16)已知 是椭圆
是椭圆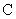 的一个焦点,
的一个焦点,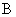 是短轴的一个端点,线段
是短轴的一个端点,线段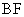 的延长线交
的延长线交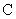 于点
于点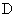 , 且
, 且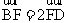 ,则
,则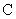 的离心率为
的离心率为
 .
.
3.第Ⅱ卷共10小题,共90分。
(1)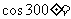
(A)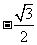 (B)-
(B)-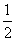 (C)
(C)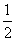 (D)
(D) 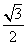
(2)设全集 ,集合
,集合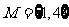 ,
,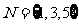 ,则
,则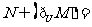
A.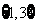 B.
B. 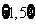 C.
C. 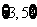 D.
D. 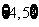
(3)若变量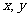 满足约束条件
满足约束条件 则
则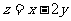 的最大值为
的最大值为
(A)4 (B)3 (C)2 (D)1
(4)已知各项均为正数的等比数列{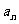 },
},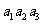 =5,
=5,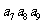 =10,则
=10,则
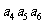 =
=
(A) 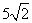 (B) 7 (C) 6 (D)
(B) 7 (C) 6 (D)
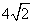
(5)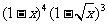 的展开式
的展开式 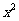 的系数为
的系数为
(A)-6 (B)-3 (C)0 (D)3
(6)直三棱柱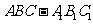 中,若
中,若 ,
,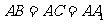 ,则异面直线
,则异面直线
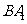 与
与 所成的角等于
所成的角等于
(A)30° (B)45°(C)60° (D)90°
(7)已知函数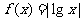 .若
.若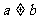 且
且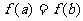 ,则
,则 的取值范围是
的取值范围是
(A) (B)
(B) (C)
(C)  (D)
(D) 
(8)已知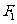 、
、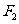 为双曲线C:
为双曲线C: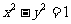 的左、右焦点,点p在C
的左、右焦点,点p在C 上,∠
上,∠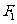 p
p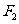 =
=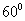 ,则
,则
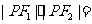
(A)2 (B)4 (C) 6 (D) 8
(9)正方体ABCD-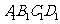 中,B
中,B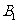 与平面AC
与平面AC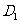 所成角的余弦值为
所成角的余弦值为
(A) 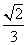 (B)
(B)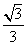 (C)
(C)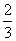 (D)
(D)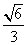
(10)设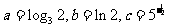 则
则
(A)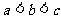 (B)
(B)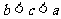 (C)
(C) 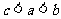 (D)
(D) 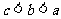
(11)已知圆O的半径为1,PA、PB为该圆的两条切线,A、B为两切点,那么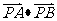 的最小值为
的最小值为
(A)  (B)
(B) (C)
(C)
 (D)
(D)
(12)已知在半径为2的球面上有A、B、C、D四点,若AB=CD=2,则四面体ABCD的体积的最大值为
(A) 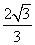 (B)
(B) (C)
(C)
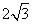 (D)
(D) 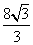
绝密★启用前
2010年普通高等学校招生全国统一考试
文科数学(必修+选修II)
第Ⅱ卷
证号填写清楚,然后贴好条形码。请认真核准条形码上的准考证号、姓名和科目。
2.第Ⅱ卷共2页,请用直径0.5毫米黑色墨水签字笔在答题卡上各题的答题区域
内作答,在试题卷上作答无效。
22.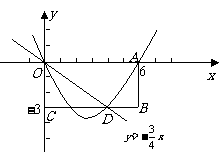 矩形
矩形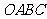 在平面直角坐标系中位置如图所示,
在平面直角坐标系中位置如图所示,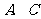 两点的坐标分别为
两点的坐标分别为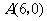 ,
,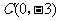 ,直线
,直线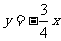 与
与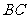 边相交于
边相交于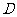 点.
点.
(1)求点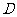 的坐标;
的坐标;
(2)若抛物线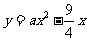 经过点
经过点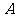 ,试确定此抛物线的表达式;
,试确定此抛物线的表达式;
(3)设(2)中的抛物线的对称轴与直线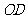 交于
交于
点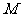 ,点
,点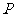 为对称轴上一动点,以
为对称轴上一动点,以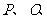
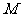 为顶点的三角形与
为顶点的三角形与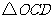 相似,求符合条件的点
相似,求符合条件的点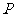 的坐标.
的坐标.
21.“六一”前夕,某玩具经销商用去2350元购进A、B、C三种新型的电动玩具共50套,并且购进的三种玩具都不少于10套,设购进A种电动玩具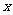 套,购进B种电动玩具
套,购进B种电动玩具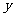 套,三种电动玩具的进价和售价如下表:
套,三种电动玩具的进价和售价如下表:
|
电动玩具型号 |
A |
B |
C |
|
进价(单位:元/套) |
40 |
55 |
50 |
|
销售价(单位:元/套) |
50 |
80 |
65 |
(1)用含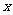 、
、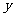 的代数式表示购进C种电动玩具的套数;
的代数式表示购进C种电动玩具的套数;
(2)求出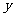 与
与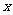 之间的函数关系式;
之间的函数关系式;
(3)假设所购进的电动玩具全部售出,且在购销这批玩具过程中需要另外支出各种费用共200元.
① 求出利润P(元)与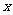 (套)之间的函数关系式;
(套)之间的函数关系式;
② 求出利润的最大值,并写出此时购进三种电动玩具各多少套?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com