
2.下列各句中,加点的成语使用正确的一项是( )
A.中国大陆赠台大熊猫“团团”、“圆圆”,正月初一在台北木栅动物园正式与游客见面,台北市十室九空,纷纷涌向动物园,一睹熊猫风采。
B.中国的经济实力大幅提升,在国际上的地位举重若轻,中美之间也已经形成了“你中有我,我中有你”的经贸合作格局,可以说,中美双方在很多领域的合作已经具有全球性的意义.
C.美华人团体声援追讨圆明园流失文物,同时促请中国政府假以辞色地与法国政府交涉,维护中华民族的尊严。
D.中央有关部门派出的调研组调研题目非常丰富,从社会分配到福利制度,从民间组织到劳资关系……可谓包罗万象。
1.下列加点字的注音全部正确的一组是( )
A. A. 老聃(dǎn) 逡巡(qùn) 黔首(qián) 朱拓(tà)
B. 从师(cónɡ) 草窠(kē) 藩篱(pān) 歆享(xīn)
C. 近谀(yú) 鞭笞(chī) 监生(jiàn) 谬种(miù)
D.膏腴(yú) 敕造(zhì) 经传(zhuàn) 罥烟(juàn)
21.(本小题满分13分)本题考查等比数列的基本知识,利用错位相减法求和等基本方法,考查抽象能力以及推理论证能力.
解:(Ⅰ)将直线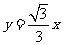 的倾斜角记为
的倾斜角记为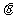 ,则有
,则有 ,
, .
.
设 的圆心为
的圆心为 ,则由题意知
,则由题意知 ,得
,得 ;同理
;同理 .
.
从而 ,将
,将 代入,解得
代入,解得 .
.
故 为公比
为公比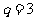 等比数列.
等比数列.
(Ⅱ)由于 ,
,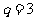 ,故
,故 ,从而
,从而 ,
,
记 ,则有
,则有 ,
①
,
①
 ②
②
①-②,得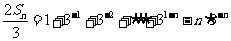

∴ .
.
21. (本小题满分13分)设
(本小题满分13分)设 ,
, ,…,
,…, ,…是坐标平面上的一列圆,它们的圆心都在
,…是坐标平面上的一列圆,它们的圆心都在 轴的正半轴上,且都与直线
轴的正半轴上,且都与直线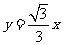 相切,对每一个正整数
相切,对每一个正整数 ,圆
,圆 都与圆
都与圆 相互外切,以
相互外切,以 表示
表示 的半径,已知
的半径,已知 为递增数列.
为递增数列.
(Ⅰ)证明: 为等比数列;
为等比数列;
(Ⅱ)设 ,求数列
,求数列 的前
的前 项和.
项和.
20.(本小题满分12分)本题考查导数的运算,利用导数研究函数的单调性与极值的方法,考查综合运用数学知识解决问题的能力.
解:由 ,知
,知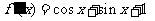 ,
,
于是 .
.
令 ,从而
,从而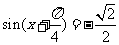 ,得
,得 ,或
,或 .
.
当 变化时,
变化时, ,
, 的变化情况如下表:
的变化情况如下表:
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
单调递增 ↗ |
 |
单调递减 ↘ |
 |
单调递增 ↗ |
因此,由上表知 的单调递增区间是
的单调递增区间是 与
与 ,单调递减区间是
,单调递减区间是 ,极小值为
,极小值为 ,极大值为
,极大值为 .
.
20.(本小题满分12分)设函数 ,求函数
,求函数 的单调区间与极值.
的单调区间与极值.
19.(本小题满分13分)本题考查空间线面平行、线面垂直、面面垂直,体积的计算等基础知识,同时考查空间想象能力与推理论证能力.
(Ⅰ)证:设 与
与 交于点
交于点 ,则
,则 为
为 的中点.连
的中点.连 、
、 ,
,
 由于
由于 为
为 的中点,故
的中点,故

 .
.
又

 ,∴
,∴

 .∴四边形
.∴四边形 为平行四边形.
为平行四边形.
∴ .而
.而 平面
平面 ,∴
,∴ 平面
平面 .
.
(Ⅱ)证:由四边形 是正方形,有
是正方形,有 .
.
又 ,∴
,∴ .而
.而 ,∴
,∴ 平面
平面 .
.
∴
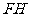 ,∴
,∴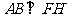 .又
.又 ,
,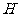 为
为 的中点,∴
的中点,∴ .
.
∴ 平面
平面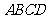 ,
,
∴ .又
.又 ,∴
,∴ .又
.又 ,
,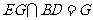 ,
,
∴ 平面
平面 .
.
(Ⅲ)解:∵ ,
,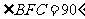 ,∴
,∴ 平面
平面 .
.
∴ 为四面体
为四面体 的高.又
的高.又 ,∴
,∴ .
.
∴ .
.
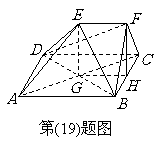
19.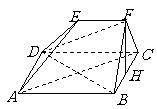 (本小题满分13分)如图,在多面体
(本小题满分13分)如图,在多面体 中,四边形
中,四边形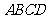 是正方形,
是正方形, ,
, ,
, ,
,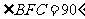 ,
, ,
,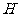 为
为 的中点.
的中点.
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)求证: 平面
平面 ;
;
(Ⅲ)求四面体 的体积.
的体积.
18.(本小题满分13分)本题考查频数,频率及频率分布直方图,考查用统计知识解决简单实际问题的能力,数据处理能力和应用意识.
解:(Ⅰ) 频率分布表: (Ⅱ)作出频率分布直方图
|
分组 |
频数 |
 频率 频率 |
 |
2 |
 |
 |
1 |
 |
 |
4 |
 |
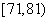 |
6 |
 |
 |
10 |
 |
 |
5 |
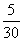 |
 |
2 |
 |
(Ⅲ)答对下述两条中的一条即可:
(ⅰ)该市一个月中空气污染指数有2天处于优的水平,占当月天数的 .有26天处于良的水平,占当月天数的
.有26天处于良的水平,占当月天数的 .处于优或良的天数共有28天,占当月天数的
.处于优或良的天数共有28天,占当月天数的 .说明该市空气质量基本良好.
.说明该市空气质量基本良好.
(ⅱ)轻微污染有2天,占当月天数的 .污染指数在80以上的接近轻微污染的天数有15天,加上轻微污染的天数,共有17天,占当月天数的
.污染指数在80以上的接近轻微污染的天数有15天,加上轻微污染的天数,共有17天,占当月天数的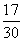 ,超过
,超过 .说明该市空气质量有待进一步改善.
.说明该市空气质量有待进一步改善.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com