
2、现有氨基酸800个,其中氨基总数为810个,羧基总数为808个,则由这些氨基酸合成的含有2条肽链的蛋白质共有肽键、氨基和羧基的数目依次分别为
A.798、2和2 B.798、12和10 C.799、1和1 D.799、11和9
1、下列各组物质的基本组成单位相同的是
A.细菌的质粒和基因 B.动物的糖元和抗原
C.人的胰岛素和性激素 D.植物的纤维素和生长素
(17)(本小题满分10分)
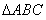 中,角A、B、C所对的边分别为
中,角A、B、C所对的边分别为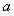 、
、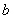 、
、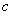 ,已知
,已知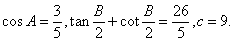
(1)求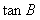 的值;
的值;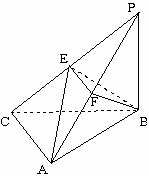 (2)求
(2)求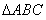 的面积。
的面积。
(18)(本小题满分12分)
如图,三棱锥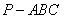 中,
中,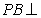 底面
底面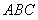 ,
,
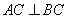 ,
,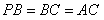 ,
,
点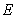 、
、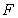 分别是
分别是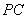 、
、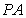 的中点.
的中点.
(Ⅰ)求证: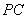 ⊥平面
⊥平面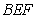 ;
;
(Ⅱ)求二面角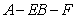 的大小.
的大小.
(19)(本小题满分12分)
已知口袋中有大小相同的n个白球和m个红球,且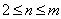 ,从袋中任意取出两个球.
,从袋中任意取出两个球.
(Ⅰ)当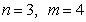 时,求取出的两个球中至少有一个红球的概率;
时,求取出的两个球中至少有一个红球的概率;
(Ⅱ)设取出的两球都是红球的概率为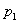 ,取出的两球恰是1红1白的概率为
,取出的两球恰是1红1白的概率为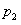 ,且
,且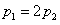 ,求证:
,求证: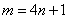 .
.
(20)(本小题满分12分)
已知函数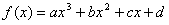 在
在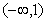 上单调递减,在(1,3)上单调递增在
上单调递减,在(1,3)上单调递增在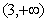 上单调递减,且函数图象在
上单调递减,且函数图象在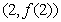 处的切线与直线
处的切线与直线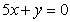 垂直.
垂直.
(Ⅰ)求实数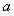 、
、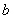 、
、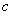 的值;
的值;
(Ⅱ)设函数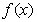 =0有三个不相等的实数根,求
=0有三个不相等的实数根,求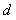 的取值范围.
的取值范围.
(21)(本题12分) 已知函数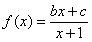 的图象过原点,且关于点(-1,1)成中心对称.
的图象过原点,且关于点(-1,1)成中心对称.
(Ⅰ)求函数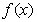 的解析式;
的解析式;
(Ⅱ)若数列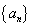
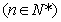 满足:
满足: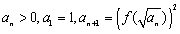 ,求数列
,求数列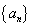 的通项
的通项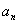 ;
;
(Ⅲ)若数列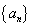 的前
的前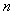 项和为
项和为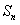 ,判断
,判断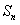 与2的大小关系,并证明你的结论.
与2的大小关系,并证明你的结论.
(22)(本小题满分12分)
设数列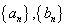 满足
满足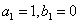 且
且
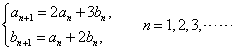
(Ⅰ)求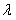 的值,使得数列
的值,使得数列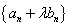 为等比数列;
为等比数列;
(Ⅱ)求数列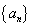 和
和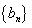 的通项公式;
的通项公式;
(Ⅲ)令数列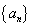 和
和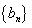 的前
的前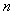 项和分别为
项和分别为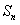 和
和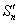 ,求极限
,求极限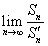 的值.
的值.
河南省实验中学2009--2010学年上期期中试卷
(13)等比数列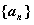 的前
的前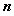 项和为
项和为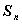 ,已知
,已知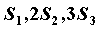 成等差数列,则
成等差数列,则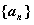 的公比为 .
的公比为 .
(14)若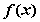 为
为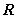 上的奇函数,且满足
上的奇函数,且满足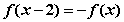 ,对于下列命题:
,对于下列命题:
①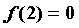 ;②
;②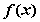 是以4为周期的周期函数;
是以4为周期的周期函数;
③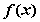 的图像关于
的图像关于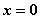 对称;④
对称;④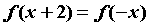 .
.
其中正确命题的序号为 .
(15)已知函数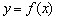 是定义在R上的奇函数,且
是定义在R上的奇函数,且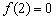 ,对任意
,对任意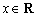 ,都有
,都有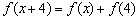 成立,则
成立,则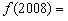 __
__.
__
__.
 (16)设常数
(16)设常数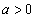 ,
,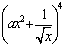 展开式中
展开式中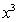 的系数为
的系数为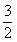 ,则
,则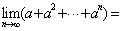 __________。
__________。
(1)计算: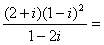 ( )
( )
A.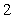 B.
B.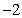 C.
C.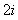 D.
D.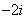
(2)已知全集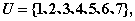
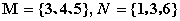 ,则集合
,则集合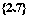 等于( )
等于( )
A.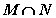 B.
B. 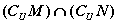 C.
C. 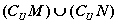 D.
D. 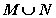
(3)下列函数中,在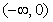 上为减函数是
( )
上为减函数是
( )
A.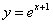 B.
B.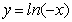 C.
C.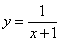 D.
D.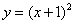
(4)已知点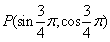 落在角
落在角 的终边上,且
的终边上,且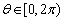 ,则
,则 的值为 ( )
的值为 ( )
A.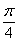 B.
B.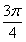 C.
C.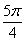 D.
D.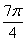
(5)在等差数列{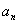 }中,
}中,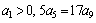 ,则使其前
,则使其前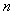 项和
项和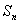 取得最大值时的
取得最大值时的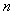 值为( )
值为( )
A.10 B.11 C.12 D.13
(6).如果函数y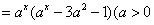 且
且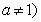 在区间
在区间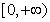 上是增函数,那么实数
上是增函数,那么实数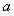 的取值范围是( )
的取值范围是( )
A.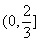 B.
B.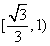 C.
C.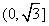 D.
D.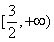
(7)已知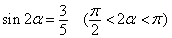 ,
,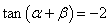 ,则
,则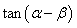 的值为 (
)
的值为 (
)
A.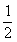 B.
B.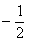 C.
C.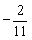 D.
D.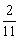
(8)若函数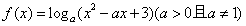 ,满足对任意的
,满足对任意的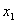 、
、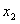 ,当
,当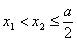 时,
时,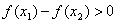 ,则实数
,则实数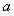 的取值范围为( )
的取值范围为( )
A.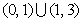 B.
B.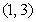 C.
C.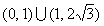 D.
D.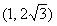
(9)给出下列命题:
①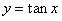 在其定义域上是增函数;
在其定义域上是增函数;
②函数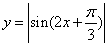 的最小正周期是
的最小正周期是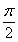 ;
;
③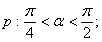
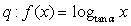 在
在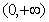 内是增函数,则
内是增函数,则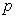 是
是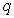 的充分非必要条件;
的充分非必要条件;
④函数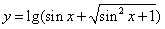 的奇偶性不能确定。
的奇偶性不能确定。
其中正确命题的序号是 ( )
A.①② B.②③ C.③④ D.①④
(10)已知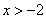 ,
,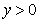 ,
,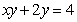 ,则
,则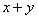 的最小值为
( )
的最小值为
( )
A.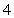 B.
B.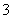 C.
C.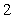 D.
D.
(11)已知函数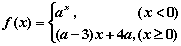 .满足对任意的
.满足对任意的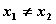 都有
都有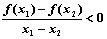 成立,则
成立,则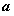 的取值范围是
( )
的取值范围是
( )
A. 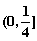 B.
B.
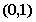 C.
C.
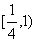 D.
D.
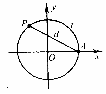
(12)如图,设点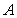 是单位圆上的一定点,动点
是单位圆上的一定点,动点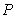 从点
从点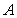 出发在圆上按逆时针方向旋转一周,点
出发在圆上按逆时针方向旋转一周,点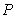 所旋转过的弧
所旋转过的弧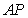 的长为
的长为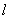 ,弦
,弦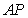 的长为
的长为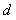 ,则函数
,则函数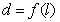 的图像大致是
( )
的图像大致是
( )
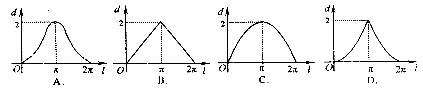
16.
 河南省实验中学2009-2010学年上期期中试卷
河南省实验中学2009-2010学年上期期中试卷
15.
14.
13.
12. 、 、
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com