
20.(本小题共14分)
已知函数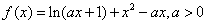 ,
,
(I)若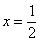 是函数
是函数 的一个极值点,求
的一个极值点,求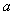 ;
;
(II)讨论函数 的单调区间;
的单调区间;
(III)若对于任意的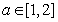 ,不等式
,不等式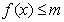 在
在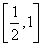 上恒成立,求
上恒成立,求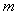 的取值范围。
的取值范围。






19.(本小题共14分)
已知二次函数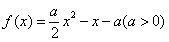
(I)若 满足条件
满足条件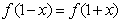 ,试求
,试求 的解析式;
的解析式;
(II)若函数 在区间
在区间 上的最小值为
上的最小值为 ,试求
,试求 的最大值。
的最大值。
18.(本小题13分)
已知函数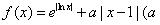 为实数)
为实数)
(I)若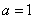 ,判断函数
,判断函数 在区间
在区间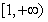 上的单调性(不必证明);
上的单调性(不必证明);
(II)若对于任意的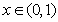 ,总有
,总有 的函数值不小于1成立,求
的函数值不小于1成立,求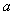 的取值范围。
的取值范围。
17.(本小题共13分)
已知向量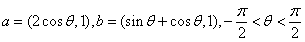
(I)若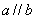 ,求
,求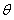 的值
的值
(II)设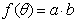 ,求函数
,求函数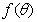 的最大值及单调递增区间。
的最大值及单调递增区间。
16.(本小题共13分)
在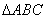 中,角
中,角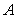 、
、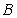 、
、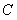 所对的边分别为
所对的边分别为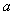 、
、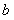 、
、 ,且
,且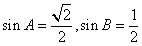
(I)求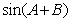 的值;
的值;
(II)若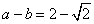 ,求
,求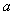 、
、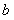 、
、 的值。
的值。
15.(本小题共13分)
已知数列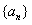 中,
中,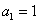 ,且点
,且点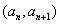 在函数
在函数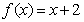 的图象上
的图象上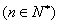 。
。
(I)求数列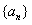 的通项公式;
的通项公式;
(II)在数列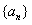 中依次取出第1项,第2项,第4项,第8项,…,第
中依次取出第1项,第2项,第4项,第8项,…,第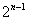 项,按取出顺序组成新的数列
项,按取出顺序组成新的数列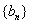 ,写出数列
,写出数列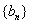 的前三项
的前三项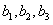 ,并求数列
,并求数列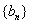 的通项
的通项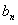 及前
及前 项和
项和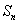 。
。
14.设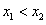 ,定义区间
,定义区间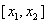 的长度为
的长度为 ,已知
,已知
函数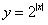 的定义域为
的定义域为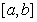 ,值域为
,值域为 ,则区间
,则区间
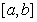 的长度的最大值与最小值的差为____________。
的长度的最大值与最小值的差为____________。
13.某学生在一个学期的数学测验成绩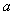 一共记录了6次
一共记录了6次
数据52,70,68,55,85,90,运行右面的程序框图
并依次将6次成绩输入,则输出的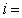 ___________,
___________,
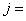 ___________,
___________,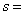 ______________。
______________。
12.已知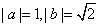 ,且
,且 ,则向量
,则向量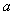 与向
与向
量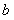 夹角的大小是______________;向量
夹角的大小是______________;向量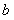 在向量
在向量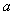 上
上
的投影是______________。
11.设函数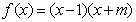 为偶函数,则
为偶函数,则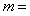
__________;函数 的零点是
的零点是 ___________。
___________。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com