
2. 数学归纳法的基本思想:即先验证使结论有意义的最小的正整数n0,如果当n=n0时,命题成立,再假设当n=k(k≥n0,k∈N*)时,命题成立.(这时命题是否成立不是确定的),根据这个假设,如能推出当n=k+1时,命题也成立,那么就可以递推出对所有不小于n0的正整数n0+1,n0+2,…,命题都成立.
1.数学归纳法:对于某些与自然数n有关的命题常常采用下面的方法来证明它的正确性:先证明当n取第一个值n0时命题成立;然后假设当n=k(kÎN*,k≥n0)时命题成立,证明当n=k+1时命题也成立 这种证明方法就叫做数学归纳法
这种证明方法就叫做数学归纳法
21.(本题14分)已知正项数列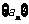 中,
中,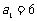 ,点
,点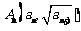 在抛物线
在抛物线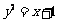 上;数列
上;数列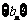 中,点
中,点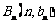 在直线
在直线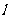 :
: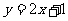 上。
上。
(1)求数列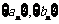 的通项公式;
的通项公式;
(2)若 ,问是否存在
,问是否存在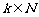 ,使
,使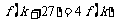
成立,若存在,求出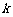 值;若不存在,说明理由;
值;若不存在,说明理由;
(3)对任意正整数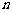 ,不等式
,不等式 成立,求正数
成立,求正数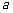 的取值范围.
的取值范围.
2009-2010学年(上)厦门理工学院附中高三数学(理科)
20. (本题14分)某家庭进行理财投资,根据长期收益率市场预测,投资债券等稳健型产品的收益与投资额成正比,投资股票等风险型产品的收益与投资额的算术平方根成正比.已知投资1万元时两类产品的收益分别为0.125万元和0.5万元(如图)。
(本题14分)某家庭进行理财投资,根据长期收益率市场预测,投资债券等稳健型产品的收益与投资额成正比,投资股票等风险型产品的收益与投资额的算术平方根成正比.已知投资1万元时两类产品的收益分别为0.125万元和0.5万元(如图)。

(1)分别写出两种产品的收益与投资的函数关系;

(2)该家庭现有20万元资金,全部用于理财投资,

问:怎样分配资金能使投资获得最大收益,其最大
收益为多少万元?
19.(本题13分)设函数 在
在 处取得极值,且曲线
处取得极值,且曲线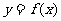 在点
在点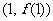 处的切线垂直于直线
处的切线垂直于直线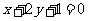 。
。

(1)求 的值;(2)若函数
的值;(2)若函数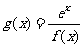 ,讨论
,讨论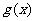 的单调性。
的单调性。









18.(本题13分)设函数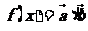 ,其中
,其中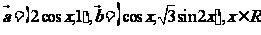


(1)求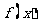 的最小正周期和最大值;(2)求
的最小正周期和最大值;(2)求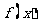 的单调递增区间。
的单调递增区间。











17.(本题13分)在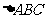 中,内角
中,内角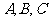 的对边分别为
的对边分别为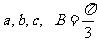 ,
,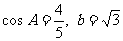 。(1)求边
。(1)求边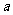 的大小;(2)求
的大小;(2)求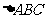 的面积。
的面积。











16.(本题13分)已知等差数列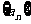 中,
中,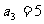 ,
,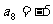 。
。

(1)求数列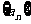 的通项公式
的通项公式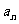 ;
;

(2)设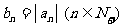 ,求数列
,求数列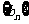 的前20项和
的前20项和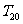 。
。









15.设定义在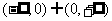 的奇函数
的奇函数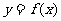 在
在 上单调递增,且
上单调递增,且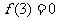 ,则
,则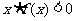 的解集是 _ ▲___。
的解集是 _ ▲___。

14.一质点受到平面上的三个力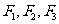 (单位:牛顿)的作用而处于平衡状态,已知
(单位:牛顿)的作用而处于平衡状态,已知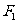 ,
,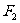 成
成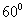 角,且
角,且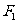 ,
,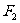 的大小分别为2和4,则
的大小分别为2和4,则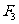 的大小为 ▲ ;
的大小为 ▲ ;

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com