3、若A={x|x=4n,n∈Z}，B={x|x=6n,n∈Z}，求A∩B.

2、设A={x|x>-2},B={x|x<0},求A∩B.

例1、(1) 若S={2，3，4}，A={4，3}，则CsA=　　　　　　　 .

　　 (2) 若S={三角形}，A={锐角三角形} ，则CsA=　　　　　　 。

　　 (3) 若U={1，3，a2+2a+1 }，A={1，3} ，则a=　　　　　　　 。

　　 　(4) 若A={0，2，4}，C_UA={-1，2}， C_UB={-1，0，2}，求B=　　　　　　　 。　

练习1：判断正误

　　　　 (1)若U={四边形}，A={梯形}，则CUA={平行四边形}

　　　　 (2)若U是全集，且AÍB，则CUAÍCUB

　　　　 (3)若U={1，2，3}，A=U，则CUA=f

思考：已知A={x|x<3}，B={x|x<a}

(1)若AÍB，C_RBÍC_RA是否成立？

(2) C_RAÍC_R(C_R(C_RB)，求a的取值范围.

例2、新华中学开运动会，设A={x|x是新华中学高一年级参加百米赛跑的同学}，B={x|x是新华中学高一年级参加跳高比赛的同学}，求A∩B .

例3、设平面内直线l₁上点的集合为L₁，直线l₂上点的集合为L₂，用集合的运算表示l₁、l₂的位置关系.

练习2：

1、设A={x|x是等腰三角形},B={x|x是直角三角形}， 求A∩B.

2、　　　　　 定义：

(1)交集：由属于集合A且属于集合B的所有元素所组成的集合，称为集合A和集合B的交集，记作A∩B，即A∩B ={x|xÎA且xÎB}.

(2)并集：由所有属于集合A或属于集合B的元素所组成的集合，称为集合A和集合B的并集，记作A∪B ，即A∪B={x|xÎA或xÎB}.

1、实例： A={a,b,c,d}　　 B={a,b,e,f}

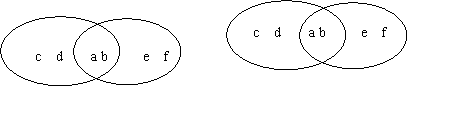
公共部分 A∩B　　　　 合并在一起 A∪B

2．例：S={1，2，3，4，5，6}　 A={1，3，5}　 C_sA ={2，4，6}

1、实例：S是全班同学的集合，集合A是班上所有参加校运会同学的集合，集合B是班上所有没有参加校运动会同学的集合.集合B是集合S中除去集合A之后余下来的集合.

结论：设S是一个集合，A是S的一个子集(即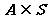)，由S中所有不属于A的元素组成的集合，叫做S中子集A的补集

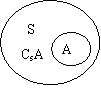记作： C_sA　　 即 C_sA ={x | xÎS且 xÏA}

定义： 如果集合S含有我们所要研究的各个集合的全部元素，

集合就可以看作一个全集.通常用U来表示.

如：把实数R看作全集U, 则有理数集Q的补集C_UQ是全体无理数的集合.

提问(板演)：用列举法表示集合：A={6的正约数}，B={10的正约数}，C={6与10的正公约数}，并用适当的符号表示它们之间的关系.

解： A={1，2，3，6}， B={1，2，5，10}， C={1，2}　 CÍA，CÍB

子集、真子集、空集的有关概念.