
1.数列极限的几种类型:∞-∞, ,0-0,
,0-0,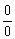 等形式,必须先化简成可求极限的类型再用四则运算求极限,另外还有先求和,约分后再求极限,对含参数的题目一定要控制好难度,不要太难了.
等形式,必须先化简成可求极限的类型再用四则运算求极限,另外还有先求和,约分后再求极限,对含参数的题目一定要控制好难度,不要太难了.
2.熟练掌握如下几个常用极限:
(1)  C=C(C为常数);
C=C(C为常数);
(2)  (
(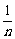 )p=0(p>0);
)p=0(p>0);
(3) 
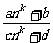 =
=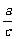 (k∈N *,a、b、c、d∈R且c≠0);
(k∈N *,a、b、c、d∈R且c≠0);
(4)  qn=0(|q|<1).
qn=0(|q|<1).
●教师下载中心
教学点睛
1.运用数列极限的运算法则求一些数列的极限时必须注意以下几点:
(1)各数列的极限必须存在;
(2)四则运算只限于有限个数列极限的运算.
9.已知数列{an}满足a1=0,a2=1,an=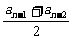 ,求
,求 an.
an.
解:由an=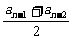 ,得
,得
2an+an-1=2an-1+an-2,∴{2an+an-1}是常数列.
∵2a2+a1=2,∴2an+an-1=2.
∴an-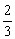 =-
=-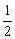 (an-1-
(an-1-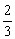 ).
).
∴{an-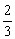 }是公比为-
}是公比为-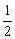 ,首项为-
,首项为-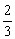 的等比数列.
的等比数列.
∴an-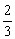 =-
=-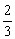 ×(-
×(-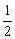 )n-1.
)n-1.
∴an=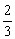 -
-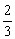 ×(-
×(-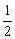 )n-1.
)n-1.
∴ an=
an=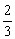 .
.
●思悟小结
8.已知数列{an}、{bn}都是由正数组成的等比数列,公比分别为p、q,其中p>q且p≠1,q≠1,设cn=an+bn,Sn为数列{cn}的前n项和,求
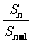 .
.
解:Sn=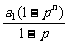 +
+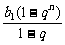 ,
,
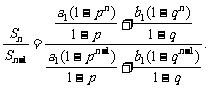
当p>1时,p>q>0,得0<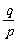 <1,上式分子、分母同除以pn-1,得
<1,上式分子、分母同除以pn-1,得
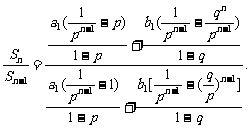
∴
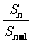 =p.
=p.
当p<1时,0<q<p<1, 
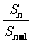 =
=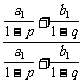 =1.
=1.
探究创新
7.已知数列{an}、{bn}都是无穷等差数列,其中a1=3,b1=2,b2是a2与a3的等差中项,且

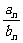 =
=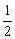 ,求极限
,求极限 (
(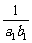 +
+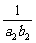 +…+
+…+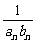 )的值.
)的值.
解:{an}、{bn}的公差分别为d1、d2.
∵2b2=a2+a3,即2(2+d2)=(3+d1)+(3+2d1),
∴2d2-3d1=2.
又
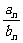 =
=
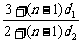 =
=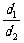 =
=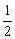 ,即d2=2d1,
,即d2=2d1,
∴d1=2,d2=4.
∴an=a1+(n-1)d1=2n+1,bn=b1+(n-1)d2=4n-2.
∴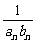 =
=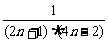 =
=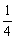 (
(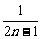 -
-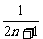 ).
).
∴原式=
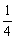 (1-
(1-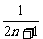 )=
)=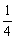 .
.
6.已知数列{an}满足(n-1)an+1=(n+1)(an-1)且a2=6,设bn=an+n(n∈N*).
(1)求{bn}的通项公式;
(2)求 (
(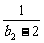 +
+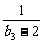 +
+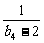 +…+
+…+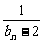 )的值.
)的值.
解:(1)n=1时,由(n-1)an+1=(n+1)(an-1),得a1=1.
n=2时,a2=6代入得a3=15.同理a4=28,再代入bn=an+n,有b1=2,b2=8,b3=18,b4=32,由此猜想bn=2n2.
要证bn=2n2,只需证an=2n2-n.
①当n=1时,a1=2×12-1=1成立.
②假设当n=k时,ak=2k2-k成立.
那么当n=k+1时,由(k-1)ak+1=(k+1)(ak-1),得a k+1=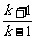 (ak-1)
(ak-1)
=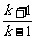 (2k2-k-1)=
(2k2-k-1)=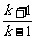 (2k+1)(k-1)=(k+1)(2k+1)=2(k+1)2-(k+1).
(2k+1)(k-1)=(k+1)(2k+1)=2(k+1)2-(k+1).
∴当n=k+1时,an=2n2-n正确,从而bn=2n2.
(2) (
(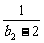 +
+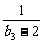 +…+
+…+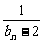 )=
)= (
(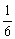 +
+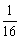 +…+
+…+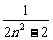 )
)
=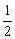
 [
[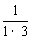 +
+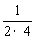 +…+
+…+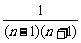 ]
]
=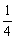
 [1-
[1-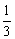 +
+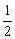 -
-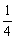 +…+
+…+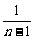 -
-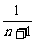 ]
]
=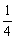
 [1+
[1+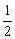 -
-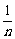 -
-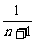 ]=
]=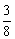 .
.
培养能力
5.(2004年湖南,理8)数列{an}中,a1=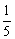 ,an+an+1=
,an+an+1=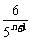 ,n∈N*,则
,n∈N*,则 (a1+a2+…+an)等于
(a1+a2+…+an)等于
A.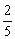 B.
B.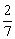 C.
C.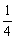 D.
D.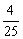
解析:2(a1+a2+…+an)=a1+[(a1+a2)+(a2+a3)+(a3+a4)+…+(an-1+an)]+an=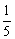 +[
+[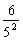 +
+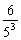 +…+
+…+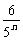 ]+an.
]+an.
∴原式=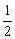 [
[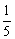 +
+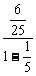 +
+ an]=
an]=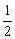 (
(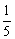 +
+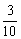 +
+ an).
an).
∵an+an+1=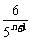 ,∴
,∴ an+
an+ an+1=0.
an+1=0.
∴ an=0.
an=0.
答案:C
4.(2004年 上海,4)设等比数列{an}(n∈N)的公比q=-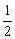 ,且
,且 (a1+a3+a5+…+a2n-1)=
(a1+a3+a5+…+a2n-1)=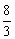 ,则a1=_________________.
,则a1=_________________.
解析:∵q=-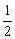 ,∴
,∴ (a1+a3+a5+…+a2n-1)=
(a1+a3+a5+…+a2n-1)=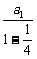 =
=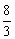 .∴a1=2.
.∴a1=2.
答案:2
3.(2004年春季上海)在数列{an}中,a1=3,且对任意大于1的正整数n,点(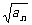 ,
,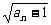 )在直线x-y-
)在直线x-y-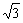 =0上,则
=0上,则
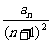 =__________________.
=__________________.
解析:由题意得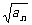 -
-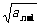 =
=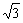 (n≥2).
(n≥2).
∴{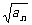 }是公差为
}是公差为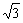 的等差数列,
的等差数列,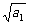 =
=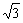 .
.
∴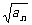 =
=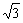 +(n-1)·
+(n-1)·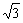 =
=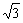 n.
n.
∴an=3n2.
∴
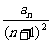 =
=
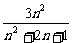
=
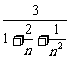 =3.
=3.
答案:3
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com