
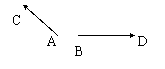 如图,老鼠由A向西北逃窜,猫在B处向东追去,设问:猫能否追到老鼠?(画图)
如图,老鼠由A向西北逃窜,猫在B处向东追去,设问:猫能否追到老鼠?(画图)
结论:猫的速度再快也没用,因为方向错了.
分析:老鼠逃窜的路线AC、猫追逐的路线BD实际上都是有方向、有长短的量.
引言:请同学指出哪些量既有大小又有方向?哪些量只有大小没有方向?
10.单摆从某点开始来回摆动,离开平衡位置的距离S(厘米)和时间t(秒)的函数关系为y= 6sin(2πt+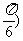 )。
)。
(1) 作出它的图象;
(2) 单摆开始摆动(t=0)时,离开平衡位置多少厘米?
(3) 单摆摆动到最右边时,离开平衡位置多少厘米?
(4) 单摆来回摆动一次需要多少时间?
9.(1)已知sinθ-cosθ=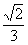
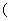 0<θ<
0<θ<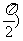 ,求sinθ+cosθ的值;
,求sinθ+cosθ的值;
(2)求函数y=2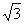 cosx+2sin2x-3的值域及取得最值是时的x的值。
cosx+2sin2x-3的值域及取得最值是时的x的值。
8.对于函数y=Asin(ωx+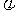 )(A、ω、
)(A、ω、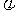 均为不等于零的常数)有下列说法:
均为不等于零的常数)有下列说法:
①最大值为A; ②最小正周期为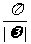 ;③在[0,2π]λο上至少存在一个x,使y=0;
;③在[0,2π]λο上至少存在一个x,使y=0;
④由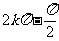 ≤ωx+
≤ωx+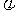 ≤
≤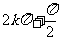 (k∈Z)解得x的范围即为单调递增区间,
(k∈Z)解得x的范围即为单调递增区间,
其中正确的结论的序号是 。
7.若函数y=a+bsinx的值域为[-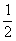 ,
,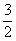 ],则此函数的解析式是 。
],则此函数的解析式是 。
6.函数y=sinx(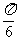 ≤x≤
≤x≤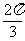 )的值域是
。
)的值域是
。
5. tan(-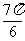 )=
.
)=
.
4. 有以下四种变换方式:
①向左平移 ,再将横坐标变为原来的
,再将横坐标变为原来的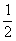 ;②将横坐标变为原来的
;②将横坐标变为原来的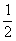 ,再向左平移
,再向左平移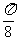 ;
;
③将横坐标变为原来的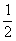 ,再向左平移
,再向左平移 ;④向左平移
;④向左平移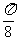 ,再将横坐标变为原来的
,再将横坐标变为原来的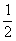 。
。
其中,能将正弦函数y=sinx的图象变为y=sin(2x+ )的图象的是( )
)的图象的是( )
A.①② B.①③ C.②③ D.②④
3.不等式tanx≤-1的解集是( )。
A.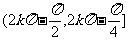 (k∈Z) B.
(k∈Z) B. 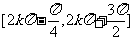 (k∈Z)
(k∈Z)
C. 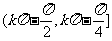 (k∈Z) D.
(k∈Z) D. 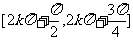 (k∈Z)
(k∈Z)
2.已知tanx=2,则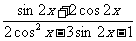 的值是( )。
的值是( )。
A.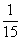 B.
B.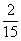 C.-
C.-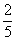 D.
D.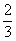
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com