
22.本小题考查两角和正切公式,倍角的正弦、余弦公式等基础知识,考查运算能力.满分12分.
解:
(I)解: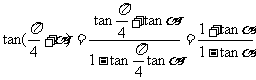
由 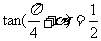 ,有
,有
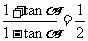
解得 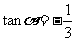 。。。。。。。。。。。。。。4分
。。。。。。。。。。。。。。4分
(II)解法一: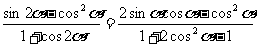 。。。。。。。。。。。。。。6分
。。。。。。。。。。。。。。6分
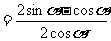
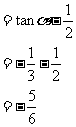 。。。。。。。。。。。。。。。12分
。。。。。。。。。。。。。。。12分
解法二:由(I),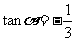 ,得
,得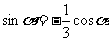
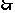
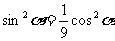
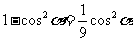
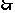
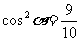 。。。。。。。。。。。。。。。。。。。。。。6分
。。。。。。。。。。。。。。。。。。。。。。6分
于是 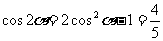 。。。。。。。。。。。。。。。。。。。。。。。8分
。。。。。。。。。。。。。。。。。。。。。。。8分
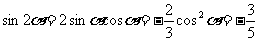 。。。。。。。。。。。。。。。10分
。。。。。。。。。。。。。。。10分
代入得
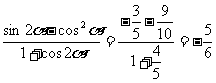 。。。。。。。。。。。。。。。。。。。。12分
。。。。。。。。。。。。。。。。。。。。12分
22.(2004. 天津卷)(本小题满分12分)
已知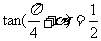
(I)求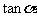 的值;
的值;
(II)
(2004. 天津卷)求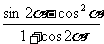 的值。
的值。
21.解:由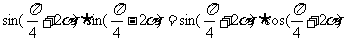
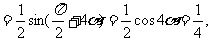
得 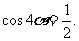 又
又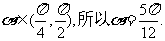
于是 
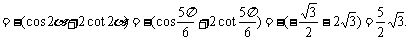
21.(2004.湖南理)(本小题满分12分)
已知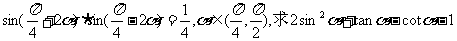 的值.
的值.
20.本小题主要考查集合的有关概念,含绝对值的不等式,简单三角函数式的化简和已知三
角函数值求角等基础知识,考查简单的分类讨论方法,以及分析问题和推理计算能力. 满
分12分.
解:(1)由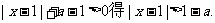
当 时,解集是R;
时,解集是R;
当 时,解集是
时,解集是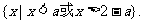 ……………………3分
……………………3分
 (2)当
(2)当 时,( ∪A)=
时,( ∪A)= ;
;
 当
当 时, ∪A=
时, ∪A=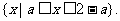 ……………………5分
……………………5分
因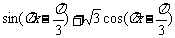
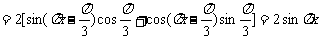
由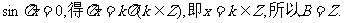 …………8分
…………8分
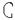 当(
∪A)∩B怡有3个元素时,a就满足
当(
∪A)∩B怡有3个元素时,a就满足 解得
解得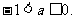 …12分
…12分
20.(2004. 辽宁卷)(本小题满分12分)
设全集U=R
(1)解关于x的不等式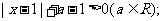
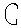 (2)记A为(1)中不等式的解集,集合
(2)记A为(1)中不等式的解集,集合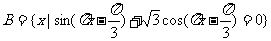 ,
,
若( ∪A)∩B恰有3个元素,求a的取值范围.
19、(2004. 上海卷文科)若tgα=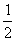 ,则tg(α+
,则tg(α+ )= 3 .
)= 3 .
18、(2004. 人教版理科)函数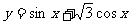 在区间
在区间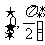 上的最小值为
.
上的最小值为
.
17.(04. 上海春季高考)在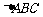 中,
中,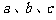 分别是
分别是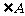 、
、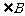 、
、 所对的边。若
所对的边。若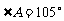 ,
,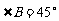 ,
,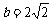 ,
则
,
则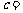 __________.2
__________.2
15. (2004. 天津卷)函数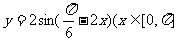 )为增函数的区间是(C )
)为增函数的区间是(C )
(A)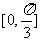 (B)
(B)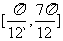 (C)
(C)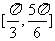 (D)
(D)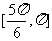
`16.(04.上海春季高考)下列函数中,周期为1的奇函数是 ( D )
(A)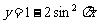 (B)
(B)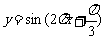 (C)
(C)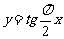 (D)
(D)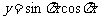
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com