
6.弧度制
①
规定:正角的弧度数为正数,负角的弧度数为负数,零角的弧度数为零。任一已知角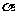 的弧度数的绝对值
的弧度数的绝对值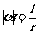 。
。
② 这种以“弧度”作为单位来度量角的制度叫做弧度制。
③
比值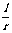 与所取圆的半径大小无关,而仅与角的大小有关。
与所取圆的半径大小无关,而仅与角的大小有关。
5. 正确理解角:“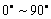 间的角”指的是:
间的角”指的是: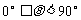 ;“第一象限的角”,“锐角”,“小于
;“第一象限的角”,“锐角”,“小于 的角”,这三种角的集合分别表示为:
的角”,这三种角的集合分别表示为:
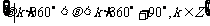 ,
,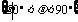 ,
,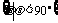 。
。
4. 与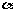 角终边相同的角的集合:
角终边相同的角的集合: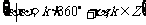
注:①终边相同的角不一定相等,但相等的角的终边一定相同;
②终边相同的角有无数多个,它们相差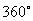 的整数倍。
的整数倍。
3. 在直角坐标系中讨论角:①角的顶点在原点,始边在x轴的非负半轴上,角的终边在第几象限,就说这个角是第几象限的角。(注意前提条件,否则不能从终边的位置来判断某角属于第几象限)。⑵若角的终边在坐标轴上,就说这个角不属于任何象限,它叫象限界角。
2. 角按其旋转方向可分为:正角,零角,负角。
㈠角的概念和弧度制
1. 角:一条射线绕着端点从一个位置旋转到另一个位置所成的图形。其中顶点,始边,终边称为角的三要素。角可以是任意大小的。
37.(福建卷)
已知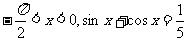 .
.
(I)求sinx-cosx的值;
(Ⅱ)求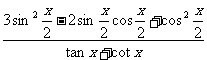 的值.
的值.
解.本小题主要考查三角函数的基本公式、三角恒等变换、三角函数在各象限符号等基本知识,以及推理和运算能力.满分12分.
解法一:(Ⅰ)由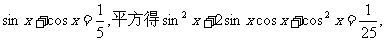
即 
又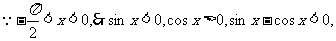 故
故 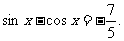
(Ⅱ)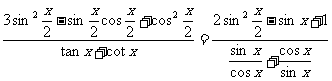
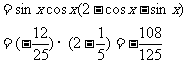
|
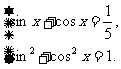
由①得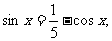 将其代入②,整理得
将其代入②,整理得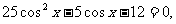
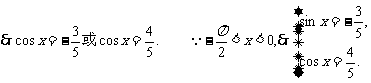 故
故 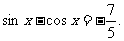
(Ⅱ)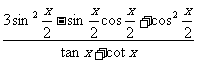
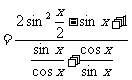
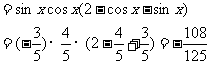
38(山东卷)已知向量
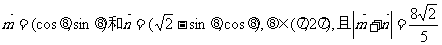 ,
,
求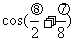 的值.
的值.
解法一:
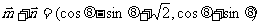

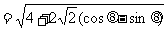
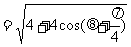
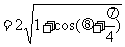
由已知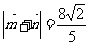 ,得
,得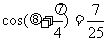
又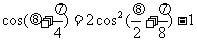
所以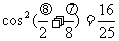
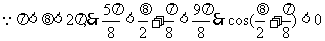
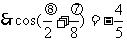
解法二:
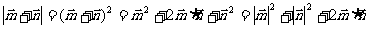

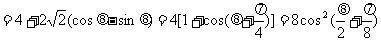
由已知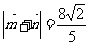 ,得
,得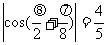
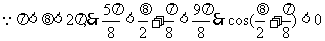
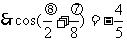
39(天津卷)
已知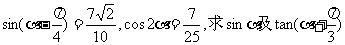 .
.
解法一:由题设条件,应用两角差的正弦公式得
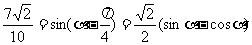
即 ①
①
由题设条件,应用二倍角余弦公式得
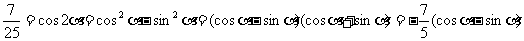 故
故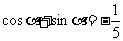 ②
②
由①式和②式得 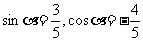 .因此,
.因此,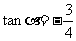 ,由两角和的正切公式
,由两角和的正切公式
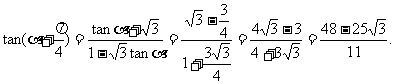
解法二:由题设条件,应用二倍角余弦公式得
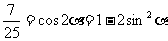
解得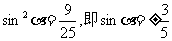
由
由于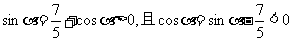 ,
,
故 在第二象限,于是
在第二象限,于是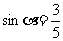 .
.
从而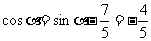
以下同解法一.
17.解: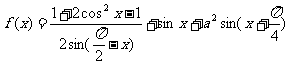
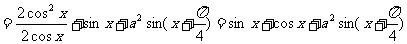
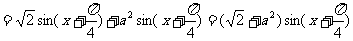
因为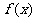 的最大值为
的最大值为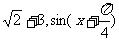 的最大值为1,则
的最大值为1,则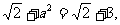
所以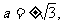
36.(重庆卷)若函数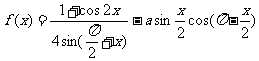 的最大值为2,试确定常数a的值.
的最大值为2,试确定常数a的值.
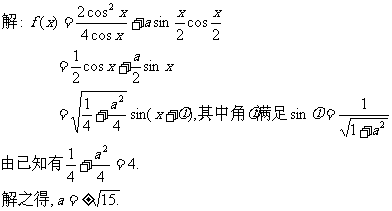 17.(重庆卷)
17.(重庆卷)
若函数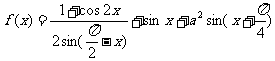 的最大值为
的最大值为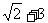 ,试确定常数a的值.
,试确定常数a的值.
35.(湖南卷)
已知在△ABC中,sinA(sinB+cosB)-sinC=0,sinB+cos2C=0,求角A、B、C的大小.
.解法一 由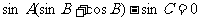 得
得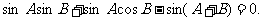
所以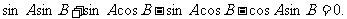 即
即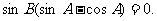
因为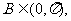 所以
所以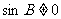 ,从而
,从而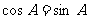
由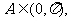 知
知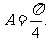 从而
从而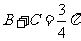 .
.
由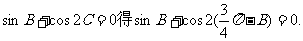
即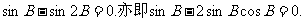
由此得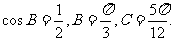 所以
所以
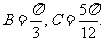
解法二:由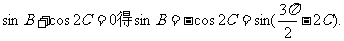
由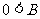 、
、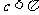 ,所以
,所以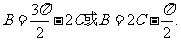 即
即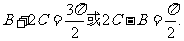
由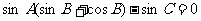 得
得 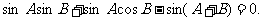
所以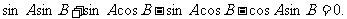
即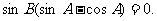 因为
因为 ,所以
,所以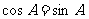
由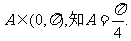 从而
从而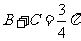 ,知B+2C=
,知B+2C=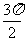 不合要求.
不合要求.
再由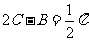 ,得
,得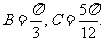 所以
所以
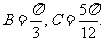
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com