
3.甲,乙两地相距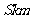 ,汽车从甲地匀速行驶到乙地,已知汽车每小时候的运输成本(单位,元),由可变部份和固定部分组成,可变部分与速度(单位:
,汽车从甲地匀速行驶到乙地,已知汽车每小时候的运输成本(单位,元),由可变部份和固定部分组成,可变部分与速度(单位: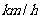 )的平方成正比,比例系数为
)的平方成正比,比例系数为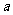 ,固定部分为
,固定部分为 元,请问,是不是汽车形驶的速度越快,其全程的运输成本就越小?如果不是,是否存在某一个汽车行驶速度,使得全程运输成本最小?
元,请问,是不是汽车形驶的速度越快,其全程的运输成本就越小?如果不是,是否存在某一个汽车行驶速度,使得全程运输成本最小?
类型六:反函数
2.设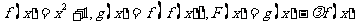 ,问是否存在实数
,问是否存在实数 ,使
,使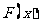 在区间
在区间 上是减函数,且在区间
上是减函数,且在区间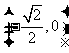 上是增函数
上是增函数
1.求函数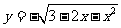 的单调递增区间
的单调递增区间
1.已知集合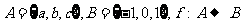 ,使得
,使得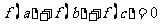 ,求映射
,求映射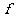 的个数
的个数
类型五:函数的单调性
3.设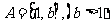 ,函数
,函数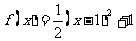 ,当
,当 ,
,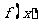 的值是
的值是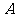 ,求
,求 的值
的值
类型四:映射
2.已知函数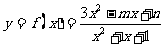 的值域是
的值域是 ,①求
,①求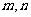 的值,②解不等式
的值,②解不等式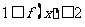
1.求 的值域
的值域
1.求 的定义域 2、求
的定义域 2、求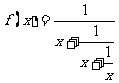 的定义域
的定义域
3.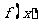 定义域是
定义域是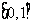 ,求
,求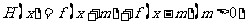 定义域
定义域
类型三:函数的值域
4.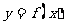 定义在R上的函数,满足
定义在R上的函数,满足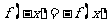 ,当
,当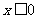 ,
, ,求
,求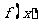 的解析式
的解析式
类型二:函数的定义域
3.若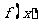 是定义在R上的函数,且
是定义在R上的函数,且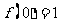 ,并且对任意的实数
,并且对任意的实数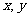 ,总有
,总有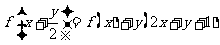 ,求
,求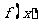 的解析式
的解析式
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com