
22.(本小题满分12分)
已知函数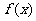 在
在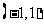 上有定义,
上有定义,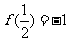 ,且满足
,且满足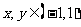 时,有
时,有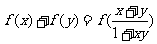 ,数列
,数列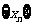 中,
中,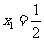 ,
,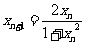 。
。
⑴ 证明: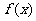 在
在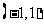 上为奇函数;
上为奇函数;
⑵求数列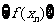 的通项公式;
的通项公式;
⑶求证: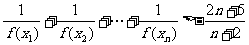
21.(本小题满分12分)
已知函数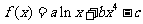 在x = 1处取得极值
在x = 1处取得极值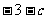 ,其中a,b,c为常数。
,其中a,b,c为常数。
⑴ 试确定a,b的值;
⑵ 讨论函数f(x)的单调区间;
⑶ 若对任意x>0,不等式 恒成立,求c的取值范围。
恒成立,求c的取值范围。
20.(本小题满分12分)
某公司计划2009年在甲、乙两个电视台做总时间不超过300分钟的广告,广告总费用不超过9万元,甲、乙电视台的广告收费标准分别为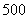 元/分钟和200元/分钟,规定甲、乙两个电视台为该公司所做的每分钟广告,能给公司带来的收益分别为0.3万元和0.2万元.问该公司如何分配在甲、乙两个电视台的广告时间,才能使公司的收益最大,最大收益是多少万元?
元/分钟和200元/分钟,规定甲、乙两个电视台为该公司所做的每分钟广告,能给公司带来的收益分别为0.3万元和0.2万元.问该公司如何分配在甲、乙两个电视台的广告时间,才能使公司的收益最大,最大收益是多少万元?
19.(本小题满分12分)
如右图所示,四棱锥P-ABCD中,底面ABCD为正方形,PD⊥平面ABCD,PD=AB=2,E,F,G分 别为PC、PD、BC的中点.
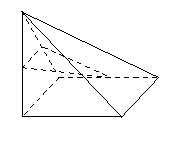 (1)求证PA∥平面EFG
(1)求证PA∥平面EFG
(2)求三棱锥P-EFG的体积.
18.(本小题满分12分)
将一颗骰子先后抛掷2次,观察向上的点数,求:
(1)两数之和为5的概率;
(2)两数中至少有一个奇数的概率;
(3)以第一次向上点数为横坐标x,第二次向上的点数为纵坐标y的点(x,y)在圆x2+y2=15的内部的概率.
17.(本小题满分10分)
已知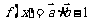 ,其中向量
,其中向量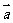 =(
=(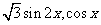 ),
),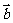 =(1,
=(1,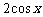 )(
)(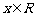 )
)
(1)求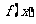 的单调递增区间;
的单调递增区间;
(2)在△ABC中,角A、B、C的对边分别为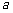 、
、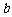 、
、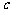 ,
,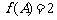 ,
,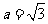 ,
,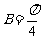 ,求边长b的值.
,求边长b的值.
16.若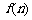 为
为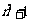 的各位数字之和
的各位数字之和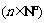 , 如: 因为
, 如: 因为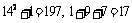 , 所以
, 所以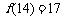 .记
.记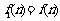 ,
,
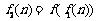 ,
…,
,
…, 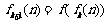 (
(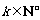 ),
则
),
则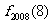 = .
= .
15.已知函数: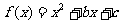 ,其中:
,其中: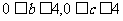 ,记函数
,记函数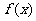 满足条件:
满足条件: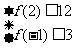 的事件为A,则事件A发生的概率为______.
的事件为A,则事件A发生的概率为______.
14.设有两个命题: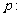 不等式
不等式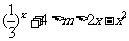 对一切实数
对一切实数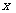 恒成立;
恒成立;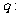
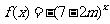 是
是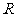 上的减函数,如果
上的减函数,如果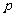 且
且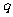 为真命题,则实数
为真命题,则实数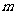 的取值范围是
_________.
的取值范围是
_________.
13.等比数列{an}共有偶数项,且所有项之和是奇数项之和的3倍,前3项之积等于27,则这个等比数列的通项公式为______________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com