
1、平面向量部分的复习应该注重向量的工具作用,紧紧围绕数形结合思想,扬长避短,解决问题;
4.已知向量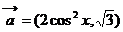 ,
, ,函数
,函数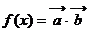 ,
,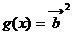 .(Ⅰ)求函数
.(Ⅰ)求函数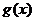 的最小正周期;(Ⅱ)在
的最小正周期;(Ⅱ)在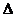
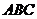 中,
中,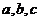 分别是角
分别是角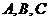 的对边,且
的对边,且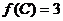 ,
,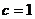 ,
,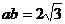 ,且
,且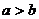 ,求
,求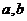 的值.
的值.
解:(Ⅰ)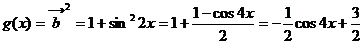
∴函数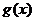 的最小周期
的最小周期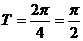
(Ⅱ)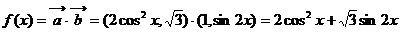
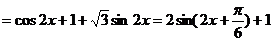
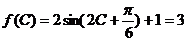
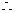
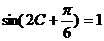
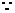
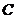 是三角形内角 ∴
是三角形内角 ∴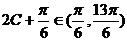 , ∴
, ∴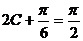 即:
即: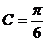
∴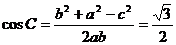 即:
即: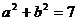 将
将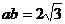 可得:
可得: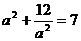 解之得:
解之得: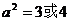 ∴
∴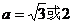
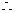
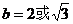
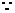
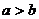 ∴
∴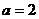
[考点预测] 2010高考预测
预计向量基本概念、向量基本运算等基础问题,通常为选择题或填空题出现;而用向量与三角函数、解三角形等综合的问题,通常为解答题,难度以中档题为主。
复习建议
2. 已知向量
已知向量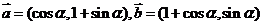 ,(1)若
,(1)若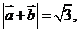 求
求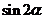 的值;(2)设
的值;(2)设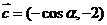 ,求
,求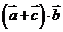 的取值范围.
的取值范围.
=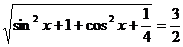
(Ⅱ)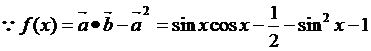
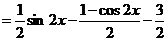
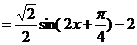 所以
所以 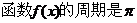
1.已知向量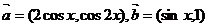
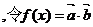 .(Ⅰ) 求 f (
.(Ⅰ) 求 f (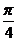 )的值;(Ⅱ)求
)的值;(Ⅱ)求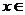
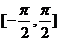 时,f (x)的单调递增区间.
时,f (x)的单调递增区间.
[解](Ⅰ) 
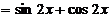 ,
,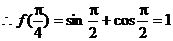
(Ⅱ) 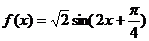 , 当
, 当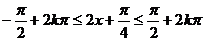 (
(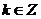 )时,f(x)单增,
)时,f(x)单增,
即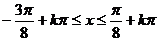 (
(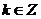 ) ∵
) ∵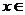
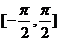 ,
,
∴  在
在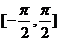 上的单调递增区间为
上的单调递增区间为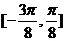 .
.
8.设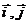 是平面直角坐标系内
是平面直角坐标系内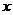 轴、
轴、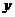 轴正方向上的单位向量,且
轴正方向上的单位向量,且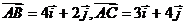 ,则
,则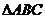 面积的值等于 ▲
面积的值等于 ▲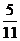 。
。
7.在平面直角坐标系中,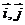 分别是与
分别是与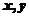 轴正方向同向的单位向量,平面内三点A、B、C满足
轴正方向同向的单位向量,平面内三点A、B、C满足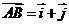 ,
,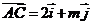 。 若A、B、C三点构成直角三角形,则实数m的值为
。 若A、B、C三点构成直角三角形,则实数m的值为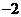 或10 .
或10 .
6.已知向量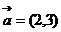 ,
,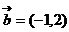 ,若
,若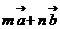 与
与 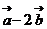 共线,则
共线,则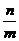 =
= 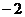 .
.
5.设点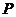 是
是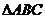 内一点(不包括边界),且
内一点(不包括边界),且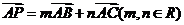 ,则
,则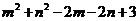 的取值范围是 (
的取值范围是 (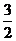 ,3)
.
,3)
.
4.
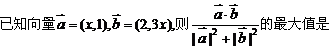
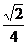
3.设 与
与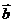 是两个不共线的向量,且向量
是两个不共线的向量,且向量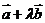 与
与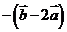 共线,则
共线,则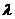 的值等于
的值等于 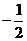
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com