22．(本题满分10分)已知函数是定义在上的奇函数,并且在上是减函数．是否存在实数使恒成立?若存在,求出实数的取值范围；若不存在，请说明理由．

21．(本题满分12分)我国是水资源比较贫乏的国家之一．目前，某市就节水问题，召开了市民听证会，并对水价进行激烈讨论，会后拟定方案如下：以户为单位，按月收缴，水价按照每户每月用水量分三级管理，第一级为每月用水量不超过12吨，每吨3．5元；第二级计量范围为超过12吨不超过18吨部分，第三级计量范围为超出18吨的部分，一、二、三级水价的单价按1：3：5计价．

　 (1)请写出每月水费(元)与用水量(吨)之间的函数关系；

　 (2)某户居民当月交纳水费为63元，该户当月用水多少吨？

20．(本题满分12分)已知函数．

　 (1)证明函数具有奇偶性；

　 (2)证明函数在上是单调函数；

　 (3)求函数在上的最值．

19．(本题满分12分)已知是二次函数，满足，求函数的解析式、值域，并写出函数的单调递减区间．

18．(本题满分12分)已知集合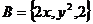，，若,求实数、的值．

17．(本题满分12分)集合，，求,,．

16．若函数满足①为偶函数；②在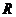上有大于零的最大值；③函数的图象过坐标原点；④，试写出一组符合要求的的值　　　 ．

15．不等式对一切实数都成立，则实数的取值范围是　　　　 　　．

14．已知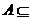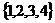，且中至少有一个偶数，则这样的有　 个．

13．函数的单调递增区间为　　　　　 ．