
15、函数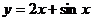 的单调增区间为
.
的单调增区间为
.
14.抛物线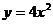 在点(1,4)处的切线方程是
.
在点(1,4)处的切线方程是
.
13.
若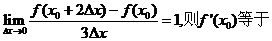 .
.
22.解:(1)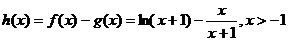 ,
,
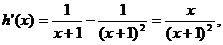 …………2分
…………2分
令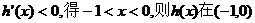 上单调递减;
上单调递减;
令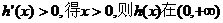 上单调递增。
上单调递增。
故增区间为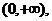 减区间为(-1,0)
减区间为(-1,0)
(2)由(1)知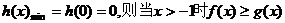 恒成立,
恒成立,

则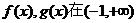 上均单调递增。 …………6分
上均单调递增。 …………6分
易知: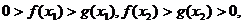
则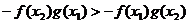 ,
,
即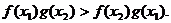 …………8分
…………8分
(3)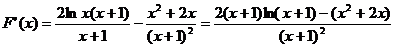 …………10分
…………10分
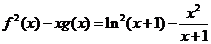
令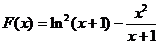
令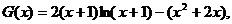
则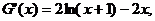
 令
令
当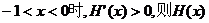 在(-1,0)上单调递增;
在(-1,0)上单调递增;
当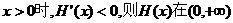 上单调递减, …………12分
上单调递减, …………12分
故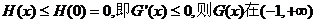 上单调递减;
上单调递减;
当
 时,
时,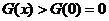 ,即
,即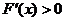 ,则
,则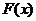 在(-1,0)上单调递增;
在(-1,0)上单调递增;
当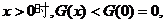
即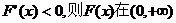 上单调递减,
上单调递减,
故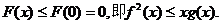 …………14分
…………14分
21.解(1)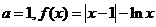
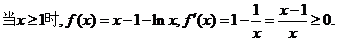
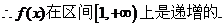 (2分)
(2分)

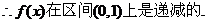
故a=1时,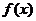 的增区间为
的增区间为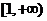 ,减区间为(0,1),
,减区间为(0,1),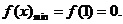 (4分)
(4分)
(2)若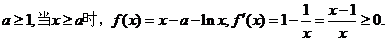
则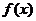 在区间
在区间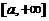 上是递增的;
上是递增的;
当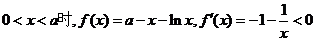
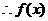 在区间
在区间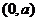 上是递减的. (5分)
上是递减的. (5分)
若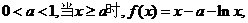
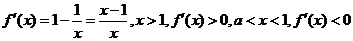
则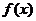 在区间
在区间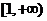 上是递增的,
上是递增的,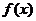 在区间
在区间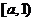 上是递减的;
上是递减的;
当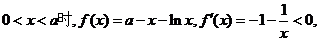
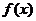 在区间(0,a)上是递减的,
在区间(0,a)上是递减的,
而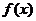 在
在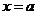 处连续;
处连续;
则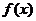 在区间
在区间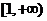 上是递增的,在区间(0,1)上是递减的 (7分)
上是递增的,在区间(0,1)上是递减的 (7分)
综上:当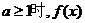 的递增区间是
的递增区间是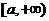 ,递减区间是(0,a);
,递减区间是(0,a);
当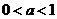 时,
时,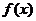 的递增区间是
的递增区间是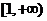 ,递减区间是(0,1) (8分)
,递减区间是(0,1) (8分)
(3)由(1)可知,当 ,
,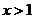 时,
时,
有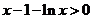 ,即
,即
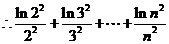
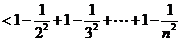
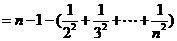
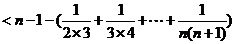
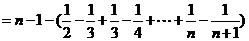
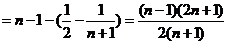 (12分)
(12分)
20.解:(1)∵由①知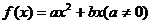 的对称轴方程是
的对称轴方程是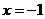 ,
,
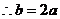 ; ………………1分
; ………………1分
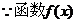 的图象与直线
的图象与直线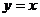 只有一个公共点
只有一个公共点 ,
,
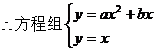 有且只有一解,
有且只有一解,
即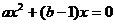 有两个相同的实根;
有两个相同的实根;
 ………………3分
………………3分
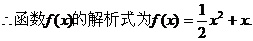 ………………4分
………………4分
(2)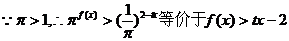 , ………………6分
, ………………6分
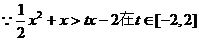 时恒成立等价于
时恒成立等价于
函数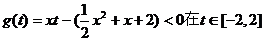 时恒成立; ………………9分
时恒成立; ………………9分
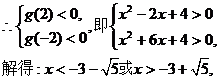
实数x的取值范围是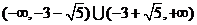 ………………12分
………………12分
19. 解:设甲项目投资x(单位:百万元),乙项目投资y(单位:百万元),两项目增加的GDP为
解:设甲项目投资x(单位:百万元),乙项目投资y(单位:百万元),两项目增加的GDP为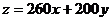 ………………1分
………………1分
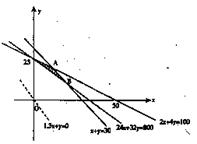
依题意,x、y满足

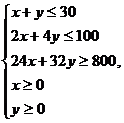 ………………5分
………………5分
所确定的平面区域如图中阴影部分 ………………8分
解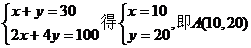
解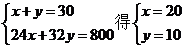 ,即B(20,10) ………………10分
,即B(20,10) ………………10分
设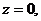 得
得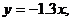 将直线
将直线 平移至经过点B(20,10),
平移至经过点B(20,10),
即甲项目投资2000万元,乙项目投资1000万元,两项目增加的GDP最大
…………12分
18.解: 上递增
上递增
即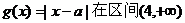 上递增, …………2分
上递增, …………2分
故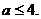 ………………4分
………………4分
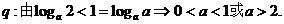 ………………8分
………………8分
如果“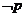 ”为真命题,则p为假命题,即
”为真命题,则p为假命题,即
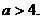 ………………9分
………………9分
又p或q为真,则q为真,即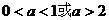
由 可得实数a的取值范围是
可得实数a的取值范围是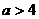 ………………12分
………………12分
22.(本小题满分14分)
已知函数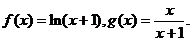
(1)求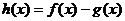 的单调区间;
的单调区间;
(2)求证:当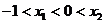 时,
时,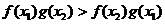 ;
;
(3)求证: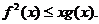
 又
又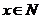 ,所以
,所以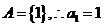 ,
,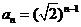 或
或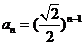 .......12分
.......12分
21.(本小题满分12分)
已知函数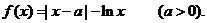
(1)若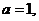 求
求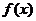 的单调区间及
的单调区间及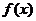 的最小值;
的最小值;
(2)求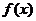 的单调区间;
的单调区间;
(3)试比较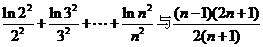 的大小,
的大小,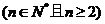 ,并证明你的结论。
,并证明你的结论。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com