
7. 设函数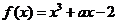 在区间
在区间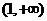 上是增函数,则实数
上是增函数,则实数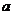 的取值范围是____
的取值范围是____
5. 三个数60.7,0.76,log0.76由小到大排列为_____________ ___
6. 函数y=log0。5(x2-3x-4)的单调减区间是______________ _____
4. 下列函数:①y=x3;②y=cosx;③y=3x;④y=ln|x|.其中既是偶函数又在(0,+∞)上单调递增的有__________________________.
3. 已知函数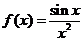 ,则
,则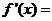 _______ _
_______ _
2.函数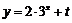 的图象不经过第二象限,则t的取值范围是 .
的图象不经过第二象限,则t的取值范围是 .
1.已知集合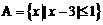 ,
,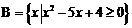 ,则
,则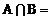 .
.
20. 已知函数f(x)=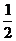 x
x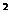 -ax+(a-1)
-ax+(a-1)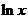 ,
,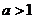 。
。
(1)讨论函数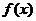 的单调性;
的单调性; 

(2)证明:若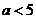 ,则对任意x
,则对任意x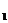 ,x
,x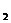
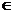
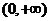 ,x
,x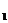
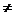 x
x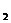 ,有
,有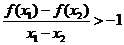 。
。
解:(1)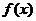 的定义域为
的定义域为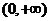 。
。
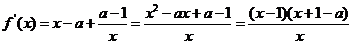 2分
2分
(i)若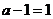 即
即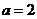 ,则
,则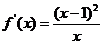 >0
>0
故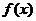 在
在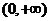 单调增加。
单调增加。
(ii)若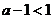 ,而
,而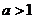 ,故
,故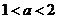 ,则当
,则当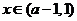 时,
时,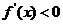 ;
;
当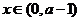 及
及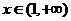 时,
时,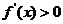
故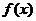 在
在 单调减少,在
单调减少,在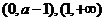 单调增加。
单调增加。
(iii)若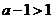 ,即
,即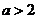 ,同理可得
,同理可得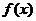 在
在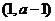 单调减少,在
单调减少,在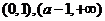 单调增加.
单调增加.
(II)考虑函数 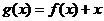
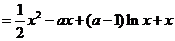
则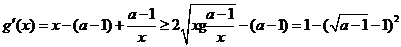
由于1<a<5,故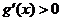 ,即g(x)在(4, +∞)单调增加,从而当
,即g(x)在(4, +∞)单调增加,从而当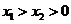 时有
时有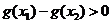 ,即
,即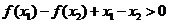 ,故
,故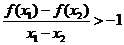 ,当
,当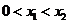 时,有
时,有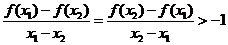 ·········16分
·········16分
南师大附校2010高三数学周末回顾测试(函数)
班级 姓名 得分
19. 设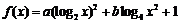 ,(
,(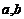 为常数).当
为常数).当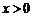 时,
时,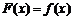 ,且
,且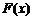 为R上的奇函数.
为R上的奇函数.
(1)若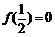 ,且
,且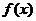 的最小值为0,求
的最小值为0,求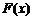 的表达式;
的表达式;
(2)在(1)的条件下,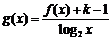 在
在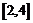 上是单调函数,求
上是单调函数,求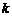 的取值范围.
的取值范围.
解: (1)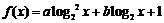
由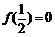 得
得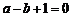 , 得
, 得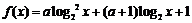
若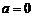 则
则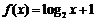 无最小值.故
无最小值.故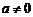 .
.
欲使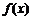 取最小值为0,只能使
取最小值为0,只能使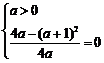 ,得
,得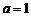 ,
,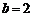 .
.
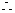
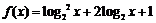 .
.
得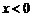 则
则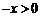 ,
,
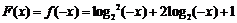 ,
,
又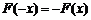 ,
,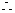
 ,
,
又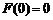
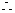
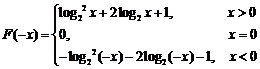
(2)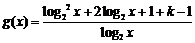
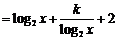 .
.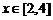 .
.
得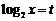 .则
.则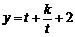 ,
,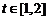 .
.
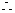 当
当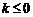 ,或
,或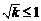 或
或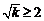 时,
时,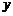 为单调函数. 综上,
为单调函数. 综上,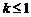 或
或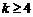 .
.
18. 统计表明,某种型号的汽车在匀速行驶中每小时的耗油量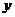 (升)关于行驶速度
(升)关于行驶速度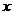 (千米/小时)的函数解析式可以表示为:
(千米/小时)的函数解析式可以表示为: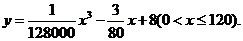 已知甲、乙两地相距100千米。
已知甲、乙两地相距100千米。
(1)当汽车以40千米/小时的速度匀速行驶时,从甲地到乙地要耗油多少升?
(2)当汽车以多大的速度匀速行驶时,从甲地到乙地耗油最少?最少为多少升?
解:(1)若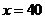 千米/小时,每小时耗油量为
千米/小时,每小时耗油量为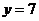 升/小时. ……2分
升/小时. ……2分
共耗油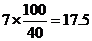 升. ………………………………4分
升. ………………………………4分
所以,从甲地到乙地要耗油17.5升. ………………………………5分
(2)设当汽车以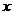 千米/小时的速度匀速行驶时耗油量最少,
千米/小时的速度匀速行驶时耗油量最少,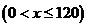 ,耗油量为S升. ………………………………6分
,耗油量为S升. ………………………………6分
则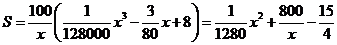 ,………………10分
,………………10分
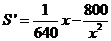 ,………………………………11分
,………………………………11分
令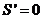 ,解得,
,解得,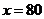 .………………………………12分
.………………………………12分
列表:
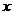 |
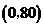 |
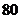 |
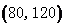 |
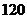 |
 |
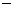 |
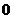 |
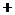 |
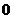 |
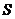 |
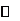 |
极小值11.25 |
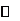 |
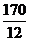 |
……………………………………………………………………………15分
所以,当汽车以80千米/小时的速度匀速行驶时,耗油量最少,为11.25升. ………………………………16分
17. 已知二次函数f(x)的二次项系数为a(a<0),且不等式f(x)>-2x的解集为(1,3).
(1)若方程f(x)+6a=0有两个相等的根,求f(x)的解析式;
(2)若f(x)的最大值为正数,求a的取值范围.
(1)因为f(x)+2x>0的解集为(1,3),所以f(x)+2x=a(x-1)(x-3),且a<0,因而
f(x)=a(x-1)(x-3)-2x=ax2-(2+4a)x+3a.①
由方程f(x)+6a=0得ax2-(2+4a)x+9a=0. ②
因为方程②有两个相等的根,所以△=2+4a)2-4a·9a=0,
即 5a2-4a-1=0,解得a=1或-.
由于a<0,所以舍去a=1.将a=-代入①得f(x)的解析式f(x)=-x2-x-.
(2)由f(x)=ax2-2(1+2a)x+3a=a(x-)2-.
及a<0,可得f(x)的最大值为-.
由解得 a<-2-或-2+<a<0.
故当f(x)的最大值为正数时,实数a的取值范围是(-∞,-2-)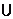 (-2+,0).
(-2+,0).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com