
2.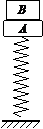 如图所示,竖直放置在水平面上的轻弹簧上放着质量为2kg的物体A,处于静止状态。若将一个质量为3kg物体B竖直向下轻放在A上的一瞬间,则B对A的压力大小(g取10m/s2) ( )
如图所示,竖直放置在水平面上的轻弹簧上放着质量为2kg的物体A,处于静止状态。若将一个质量为3kg物体B竖直向下轻放在A上的一瞬间,则B对A的压力大小(g取10m/s2) ( )

A. 30N B.0 C.12N D.15N
30N B.0 C.12N D.15N
1.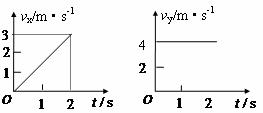 质量为1kg的物体在水平面内做曲线运动,已知互相垂直方向上的速度图象分别如图所示.下列说法正确的是( )
质量为1kg的物体在水平面内做曲线运动,已知互相垂直方向上的速度图象分别如图所示.下列说法正确的是( )
A.质点的初速度为5m/s
B.质点所受的合外力为3N
C.2s末质点速度大小为7m/s
D.质点初速度的方向与合外力方向垂直
21.(14分)已知函数f (x)=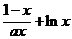 。
。
( 1)若函数f (x)在[1,+∞)上为增函数,求正实数
1)若函数f (x)在[1,+∞)上为增函数,求正实数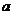 的取值范围;
的取值范围;
(2)当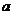 =1时,求f
(x)在[
=1时,求f
(x)在[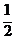 ,2]上的最大值和最小值。
,2]上的最大值和最小值。
(3)求证:对于大于1的正整数n,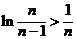 。
。
20.(13分)已知各项均为正数的数列{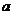 n }的前n项和Sn满足S1>1,且6Sn=(
n }的前n项和Sn满足S1>1,且6Sn=(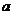 n +
n + 1)(
1)(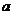 n +2) (
n +2) ( n为正整数)。
n为正整数)。
(1)求{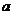 n}的通项公式;
n}的通项公式;
(2)设数列{bn}满足bn=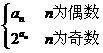 ,求Tn=b1+ b2+…+bn;
,求Tn=b1+ b2+…+bn;
19.(12分)某处森林发生火灾,火势正以每分钟100m2的速度顺风蔓延,消防站接到警报立即调派消防员赶往火场,在火灾发生后五分钟到达救火现场,已知消防队员在现场平均每人每分钟灭火50m2,所消耗的灭火材料、劳务津贴等费用为每人每分钟125元,另附加每次救火所耗损的车辆、器械和装备等费用平均每人100元,而烧毁1m2森林损失费为60元,问应该派多少消防队员前去救火,才能使总的损失最少?
18.(12分)已知不等式mx2-2mx+m-1<0。
(1)若对所有的实数x不等式恒成立,求m的取值范围;
(2)设不等式对于满足|m|<2的一切m的值都成立,求x的取值范围。
16.(12分)已知函数f(x)=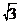 sinωxcosωx-cos2ωx-
sinωxcosωx-cos2ωx-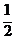 (x∈R,ω>0)。
(x∈R,ω>0)。
(1)若f (x)的图象中相邻的两条对称轴之间的距离不小于
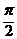 ,求ω的取值范围;
,求ω的取值范围;
(2)若f (x)的最小正周期为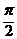 ,求函数f (x)的最大值,并且求出使f (x)取得最大值的x的集合。
,求函数f (x)的最大值,并且求出使f (x)取得最大值的x的集合。
17 .(12分)已知向量
.(12分)已知向量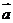 =(
=(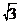 ,-1),
,-1),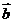 =(
=(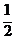 ,
,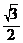 )且存在实数k和t使
)且存在实数k和t使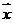 =
=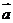 +(t2-3)
+(t2-3)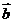 ,
,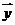 =-k
=-k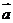 + t
+ t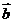 ,若
,若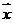 ⊥
⊥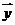 ,试求
,试求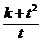 的最小值。
的最小值。
15.函数f(x)=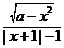 为奇函数,则实数a的取值
为奇函数,则实数a的取值 范围是
;
范围是
;
14.已知向量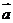 与
与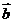 的夹角为120º,若向量
的夹角为120º,若向量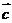 =
=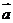 +
+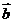 ,且
,且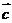 ⊥
⊥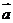 ,则
,则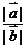 的值为 ;
的值为 ;
13.把函 数
数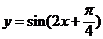 的图象向右平移
的图象向右平移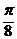 个单位,再把所得图象上各点的横坐标变为原来的
个单位,再把所得图象上各点的横坐标变为原来的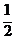 (纵坐标不变),则所得图象的解
(纵坐标不变),则所得图象的解 析式为
;
析式为
;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com