
12.已知点P(x,y)满足条件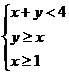 ,则x2+y2的值域为 ;
,则x2+y2的值域为 ;
11.设等差数列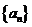 的前
的前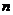 项和为
项和为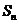 ,若
,若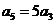 则
则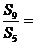 ;
;
10.定义在R上的偶函数f(x)满足f(x+2)=f(x),且f(x)在[-3,-2]上是减函数,又α、β是锐角三角形的两个内角,则
A、f(sinα)>f(sinβ) B、f(cosα)<f(cosβ)
C、f(sinα)<f(cosβ) D、f(sinα)>f(cosβ)
9. 设函数f(x)定义如下表,数列{xn}满足x0=5,且对任意的自然数n均有xn+1=f(xn),则x2009等于
设函数f(x)定义如下表,数列{xn}满足x0=5,且对任意的自然数n均有xn+1=f(xn),则x2009等于
|
x |
1 |
2 |
3 |
4 |
5 |
|
f(x) |
4 |
1 |
3 |
5 |
2 |
A、1 B、2 C、4 D、5
8.在⊿ABC中,若(a-c•cosB)sinB=(b-c•cosA)sinA,则这个三角形是
A、等腰三角形 B、直角三角形
C、等腰或直角三角形 D、等腰直角三角形
7.函数f(x)=(x-3)ex的单调递增区间是
A、(2,+∞) B、(0,3) C、(1,4) D、(-∞,2)
6.已知等比数列{an}满足an>0,n=1,2,…,且a5•a2n-5=22n (n≥3),则当n≥1时,
log2a1+log2a3+…+log2a2n-1=
A、n(2n- 1) B、(n+1)2 C、n2 D、(n-1)2
1) B、(n+1)2 C、n2 D、(n-1)2
5.已知tan(α+β+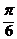 )=
)=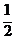 ,tan(β-
,tan(β-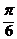 )=-
)=-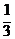 ,则tan(α+
,则tan(α+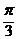 )等于
)等于
A、1 B、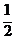 C、2 D、
C、2 D、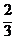
4.已知三个互不相等的实数a,b,c成等差数列,那么关于x的方程ax2+2bx+c=0
A、一定有两个不相等的实数根 B、一定有两个相等的实数根
C、一定没有实数根 D、一定有实数根
3.给出下面结论:①命题p:“∃x∈R,x2-3x+2≥0”的否定为¬p:“∀x∈R,x2-3x+2<0”;
②命题:“∀x∈M,P(x)”的否定为:“∃x∈M, P(x)”; ③若¬p是q的必要条件,则p是¬q的充分条件;
④“M>N”是“㏒aM>㏒aN”的充分不必要条件。其中正确结论的个数为
P(x)”; ③若¬p是q的必要条件,则p是¬q的充分条件;
④“M>N”是“㏒aM>㏒aN”的充分不必要条件。其中正确结论的个数为
A、4 B、3 C、2 D、1
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com