
9.★★★★某城市理论预测2000年到2005年人口总数与年份的关系如下表所示
|
年份x |
2000 |
2001 |
2002 |
2003 |
2004 |
2005 |
|
人口数y万 |
50 |
69 |
88 |
110 |
190 |
350 |
(1) 画出散点图,试建立y与x之间的回归方程.
(2) 据此估计2006年人口总数.
(3) 计算相关指数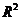 、残差、残差平方和.
、残差、残差平方和.
8.★★★★(教材1.1例2变式2)为了研究某种细菌随时间x变化,繁殖的个数,收集数据如下:
|
天数x/天 |
1 |
2 |
3 |
4 |
5 |
6 |
|
繁殖个数y/个 |
6 |
12 |
25 |
49 |
95 |
190 |
(1) 用天数作解释变量,繁殖个数作预报变量,作出这些数据的散点图
(2) 求出回归方程
(3) 描述解释变量与预报变量之间的关系,计算残差、相关指数R2.
实践演练
7.★★★(教材1.1例2变式1)在彩显影中,由经验可知:形成染料光学密度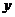 与析出银的光学密度
与析出银的光学密度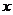 由公式
由公式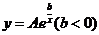 表示。现测得试验数据如下:
表示。现测得试验数据如下:
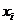 |
0.05 |
0.06 |
0.25 |
0.31 |
0.07 |
0.10 |
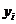 |
0.10 |
0.14 |
1.00 |
1.12 |
0.23 |
0.37 |
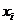 |
0/38 |
0.43 |
0.14 |
0.20 |
0.47 |
|
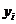 |
1.19 |
1.25 |
0.59 |
0.79 |
1.29 |
|
试求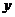 对
对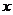 的回归方程。
的回归方程。
6.★★★若某函数模型相对一组数据的残差平方和为89,其相关指数为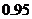 ,则总偏差平方和为
,则总偏差平方和为
变式活学
5.★★某医院用光电比色检验尿汞时,得到尿汞含量(毫克/升)与消化系数如下表:
尿汞含量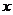 |
2 |
4 |
6 |
8 |
10 |
|
消化系数 |
64 |
138 |
205 |
285 |
260 |
若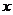 与
与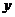 具有线性相关关系,则回归直线方程是 。
具有线性相关关系,则回归直线方程是 。
4.★有下列关系:
(1)人的年龄与他(她)拥有的财富之间的关系;
(2)曲线上的点与该点的坐标之间的关系;
(3)苹果的产量与气候之间的关系;
(4)森林中的同一种树木,其断面直径与高度之间的关系;
(5)学生与他(她)的学号之间的关系。
其中有相关关系的是 (填写你认为正确的序号).
3.★★★设两个变量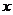 与
与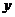 之间具有线性相关关系,它们的相关系数是
之间具有线性相关关系,它们的相关系数是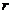 ,
,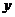 关于
关于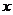 的回归直线方程的斜率是
的回归直线方程的斜率是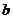 ,纵载距是
,纵载距是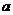 ,那么必有( )
,那么必有( )
A.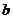 与
与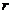 符号相同 B.
符号相同 B.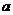 与
与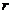 符号相同
符号相同
C.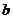 与
与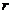 符号相反 D.
符号相反 D.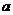 与
与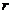 符号相反
符号相反
2.★★在回归分析中,关于残差的有以下几种说法:
①分析残差可以寻找异常点,就是残差比较大的点,以便于考察相应的样本数据是否有错
②分析残差图可以发现模型选择是否合适
③分析残差可以考察是否有其它变量需要加入到模型中
④分析残差可以发现模型假设是否正确
⑤残差与残差图可以帮助判断模型的拟合效果
其中说法正确的个数为( )
A.3个 B.4个 C.5个 D.2个
1.★★如果散点图中所有的样本点均在同一条直线上,那么残差平方和与相关系数分别为( )
A.1,0 B.0,1
C.0.5,0.5 D.0.43,0.57
3.1回归分析的基本思想及其初步应用(3)
双基再现
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com