
4.(2008-2009学年度徐闻一中高三化学第三次测) 2008年9月11日,全国各地多处发现婴儿因食用三鹿奶粉而出现肾结石的事件。当晚,三鹿集团承认婴幼儿奶粉受到三聚氰胺污染,并宣布召回市面上被污染的产品。三聚氰胺的分子结构如下:有关三聚氰胺的说法正确的是( )
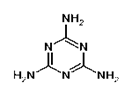 A.三聚氰胺属于芳香族化合物,但不属于芳香烃;
A.三聚氰胺属于芳香族化合物,但不属于芳香烃;
B.三聚氰胺的分子式为C3N6H6;
C.三聚氰胺中的碳原子属于饱和碳原子;
D.三聚氰胺分子中的所有原子都在一个平面内
3.(深圳市沙头角中学2009年高三1月测试题)下列关于有机物的说法正确的是
A.乙醇、乙烷和乙酸都可以与钠反应生成氢气
B.75%(体积分数)的乙醇溶液常用于医疗消毒
C.苯和乙烯都可使溴的四氯化碳溶液褪色
D.石油分馏可获得乙酸、苯及其衍生物
2.(深圳市沙头角中学2009年高三1月测试题)有关天然产物水解的叙述不正确的是
A.油脂水解可得到丙三醇 B.可用碘检验淀粉水解是否完全
C.蛋白质水解的最终产物均为氨基酸 D.纤维素水解与淀粉水解得到的最终产物不同
1.(惠州市2009届高三第二次调研考试)下列有关物质分类的说法中正确的是
A.石英玻璃、普通玻璃都属于硅酸盐 B.CH2Cl2、C2H6都是纯净物
C.煤、石油都属于可再生能源 D.纯碱、烧碱都属于碱类物质
17.设函数f (x)= ln(x+a)+x2
(1)若当x=-1时,f (x)取得极值,求a的值,并讨论f (x)的单调性.
(2)若f (x)存在极值,求a的取值范围,并证明所有极值之和大于ln.
解:(1)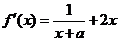 ,
,
依题意有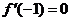 ,故
,故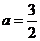 .
.
从而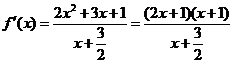 .
.
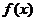 的定义域为
的定义域为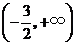 ,当
,当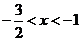 时,
时,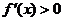 ;
;
当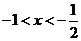 时,
时,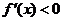 ;
;
当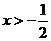 时,
时,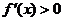 .
.
从而,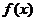 分别在区间
分别在区间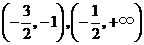 单调增加,在区间
单调增加,在区间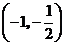 单调减少.
单调减少.
(2)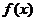 的定义域为
的定义域为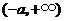 ,
,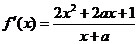 .
.
方程 的判别式
的判别式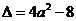 .
.
(ⅰ)若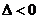 ,即
,即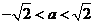 ,在
,在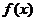 的定义域内
的定义域内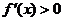 ,故
,故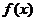 的极值.
的极值.
(ⅱ)若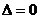 ,则
,则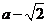 或
或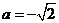 .
.
若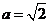 ,
,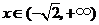 ,
,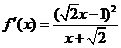 .
.
当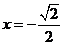 时,
时,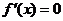 ,当
,当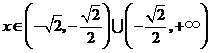 时,
时,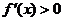 ,所以
,所以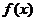 无极值.
无极值.
若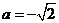 ,
,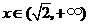 ,
,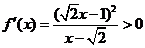 ,
,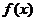 也无极值.
也无极值.
(ⅲ)若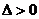 ,即
,即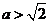 或
或 ,则
,则 有两个不同的实根
有两个不同的实根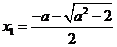 ,
,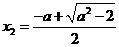 .
.
当 时,
时,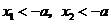 ,从而
,从而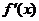 有
有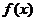 的定义域内没有零点,故
的定义域内没有零点,故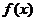 无极值.
无极值.
当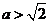 时,
时,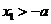 ,
,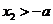 ,
,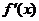 在
在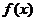 的定义域内有两个不同的零点,由根值判别方法知
的定义域内有两个不同的零点,由根值判别方法知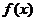 在
在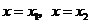 取得极值.
取得极值.
综上,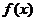 存在极值时,
存在极值时,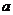 的取值范围为
的取值范围为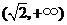 .
.
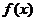 的极值之和为
的极值之和为
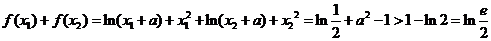
16.在直角坐标系xoy中,已知圆心在第二象限、半径为2的圆C与直线y=x相切于坐标原点O,椭圆+=1与圆C的一个交点到椭圆两焦点的距离之和为10.
(1)求圆C的方程;
(2)试探究圆C上是否存在异于原点的点Q,使Q到椭圆的右焦点F的距离等于线段OF的长,若存在求出Q的坐标;若不存在,请说明理由.
解:(1)圆C: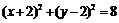 ;
;
(2)由条件可知a=5,椭圆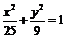 ,∴F(4,0),若存在,则F在OQ的中垂线上,又O、Q在圆C上,所以O、Q关于直线CF对称;
,∴F(4,0),若存在,则F在OQ的中垂线上,又O、Q在圆C上,所以O、Q关于直线CF对称;
直线CF的方程为y-1=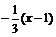 ,即
,即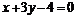 ,设Q(x,y),则
,设Q(x,y),则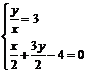 ,解得
,解得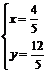
所以存在,Q的坐标为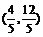 .
.
15.某分公司经销某种品牌产品,每件产品的成本为3元,并且每件产品需向总公司交a
元(3≤a≤5)的管理费,预计当每件产品的售价为x元(9≤x≤11)时,一年的销售量为(12-x)2万件.
(1)求分公司一年的利润L(万元)与每件产品的售价x的函数关系式;
(2)当每件产品的售价为多少元时,分公司一年的利润L最大,并求出L的最大值.
解:(1)分公司一年的利润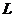 (万元)与售价
(万元)与售价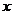 的函数关系式为:
的函数关系式为:
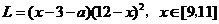 .
.
(2)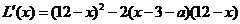
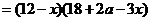 .
.
令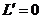 得
得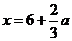 或
或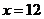 (不合题意,舍去).
(不合题意,舍去).
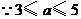 ,
,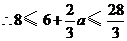 .
.
在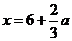 两侧
两侧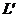 的值由正变负.
的值由正变负.
所以(1)当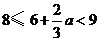 即
即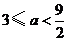 时,
时,
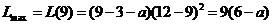 .
.
(2)当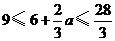 即
即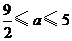 时,
时,
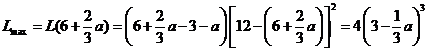 ,
,
所以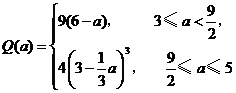
答:若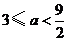 ,则当每件售价为9元时,分公司一年的利润
,则当每件售价为9元时,分公司一年的利润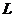 最大,最大值
最大,最大值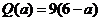 (万元);若
(万元);若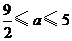 ,则当每件售价为
,则当每件售价为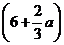 元时,分公司一年的利润
元时,分公司一年的利润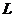 最大,最大值
最大,最大值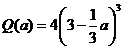 (万元).
(万元).
14.如图,在直四棱柱ABCD-A1B1C1D1中,已知DC=DD1=2AD=2AB,AD⊥DC,AB∥DC,E为DC的中点.
(1)求证:D1C⊥AC1;
(2)D1E∥平面A1BD.
13.已知cosa=,cos(a-b)=,且0<b<a<.
(1)求tan2a的值; (2)求角b的值.
解:(1)由cosa=,0<a<,得sina=.所以tana==4,tan2a==-.
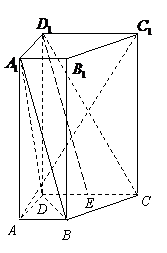 (2)由0<b<a<得0<a-b<,又cos(a-b)=,所以sin(a-b)=.cosb=cos[a-(a-b)]=cosacos(a-b)+sinasin(a-b)=×+×=,所以b=.
(2)由0<b<a<得0<a-b<,又cos(a-b)=,所以sin(a-b)=.cosb=cos[a-(a-b)]=cosacos(a-b)+sinasin(a-b)=×+×=,所以b=.
12.已知曲线C:y=2x2,点A(0,-2)及点B(3,a),从点A观察点B,要使视线不被C挡住,则实数a的取值范围是_______________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com