2.在证明平行时注意线线平行、线面平行及面面平行判定定理和性质定理的反复运用.

1.斜线与平面所成的角关键在于找射影，斜线与平面所成的角，是这条斜线和这个平面内的直线所成的一切角中最小的角.

7.　　 从平面外一点向这个平面所引的垂线段和斜线段中：①射影相等的两条斜线段相等，射影较长的斜线段也较长；②相等的斜线段的射影相等，较长的斜线段的射影也较长；③垂线段比任何一条斜线段都短.

6.　　 三垂线定理(在平面内的一条直线，如果和这个平面的一条斜线在这个平面内的射影垂直，那么它也和这条斜线垂直)、逆定理(在平面内的一条直线，如果和这个平面的一条斜线垂直，那么它也和这条斜线在这个平面内的射影垂直).

5.　　 直线与平面的距离(一条直线和一个平面平行时，这条直线上任意一点到这个平面的距离，叫做这条直线和这个平面的距离).

4.　　 直线与平面垂直的定义是：如果一条直线和一个平面内所有直线垂直，那么这条直线和这个平面垂直；掌握直线与平面垂直的判定定理(如果一条直线和平面内的两条相交直线都垂直，那么这条直线垂直于这个平面)和性质定理(如果两条直线同垂直于一个平面，那么这两条直线平行).

3.　　 掌握直线与平面平行判定定理(如果平面外的一条直线和平面内的一条直线平行，那么这条直线和平面平行)和性质定理(如果一条直线和一个平面平行，经过这条直线的平面和这个平面相交，那么这条直线和交线平行).

2.　　 直线和平面所成的角，当直线与平面平行或在平面内时所成的角是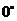，当直线与平面垂直时所成的角是9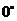，当直线与平面斜交时所成的角是直线与它在平面内的射影所成的锐角.

1.　　 掌握空间直线与平面的三种位置关系(直线在平面内、相交、平行).

7．如图正四面体中，D、E是棱PC上不重合的两点；F、H分别是棱PA、PB上的点，且与P点不重合．

求证：EF和DH是异面直线．

§6.2直线与平面之间的位置关系