
4.相反向量:我们把与向量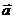 长度相等,方向相反的向量叫做
长度相等,方向相反的向量叫做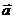 的相反向量。记作-
的相反向量。记作-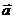 。
。
3.相等向量:长度相等且方向相同的向量。
2.平行向量:方向相同或相反的非零向量叫做平行向量,又叫做共线向量。
1.模(长度):向量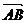 的大小,记作|
的大小,记作|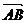 |。长度为0的向量称为零向量,长度等于1个单位长度的向量,叫做单位向量。
|。长度为0的向量称为零向量,长度等于1个单位长度的向量,叫做单位向量。
5.已知椭圆的中心在原点,离心率为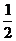 ,一个焦点是F(-m,0)(m是大于0的常数).
,一个焦点是F(-m,0)(m是大于0的常数).
(1)求椭圆的方程;
(2)设Q是椭圆上的一点,且过点F、Q的直线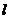 与
与 轴交于点M. 若|MQ|=2|QF|,求直线
轴交于点M. 若|MQ|=2|QF|,求直线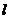 的斜率.
的斜率.
第八章 平面向量与空间向量
§8.1平面向量及其运算
4.已知倾斜角为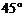 的直线
的直线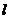 过点A(1,-2)和点B,B在第一象限,|AB|=3
过点A(1,-2)和点B,B在第一象限,|AB|=3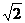 .
.
(1) 求点B的坐标;
(2) 若直线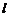 与双曲线
与双曲线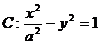
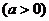 相交于
相交于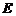 、
、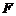 两点,且线段
两点,且线段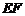 的中点坐标为(4,1),求
的中点坐标为(4,1),求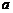 的值;
的值;
(3) 对于平面上任一点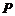 ,当点Q在线段AB上运动时,称|PQ|的最小值为
,当点Q在线段AB上运动时,称|PQ|的最小值为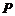 与线段
与线段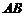 的距离. 已知点
的距离. 已知点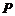 在
在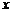 轴上运动,写出点
轴上运动,写出点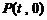 到线段
到线段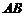 的距离
的距离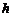 关于
关于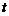 的函数关系式.
的函数关系式.
3.直线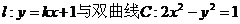 的右支交于不同的两点A、B.
的右支交于不同的两点A、B.
(1)求实数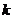 的取值范围;
的取值范围;
(2)是否存在实数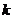 ,使得以线段AB为直径的圆经过双曲线C的右焦点F?若存在,求出
,使得以线段AB为直径的圆经过双曲线C的右焦点F?若存在,求出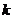 的值;若不存在,说明理由.
的值;若不存在,说明理由.
2.制定投资计划时,不仅要考虑可能获得的盈利,而且要考虑可能出现的亏损.某投资人打算投资甲、乙两个项目. 根据预测,甲、乙项目可能的最大盈利率分别为100﹪和50﹪,可能的最大亏损分别为30﹪和10﹪. 投资人计划投资金额不超过10万元,要求确保可能的资金亏损不超过1.8万元. 问投资人对甲、乙两个项目各投资多少万元,才能使可能的盈利最大?
1.过抛物线 2=4
2=4 的对称轴上任一点P(0,m)(m>0)作直线与抛物线交于A,B两点,点Q是点P关于原点的对称点.
的对称轴上任一点P(0,m)(m>0)作直线与抛物线交于A,B两点,点Q是点P关于原点的对称点.
(1)设点P分有向线段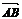 所成的比为
所成的比为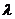 ,证明:
,证明:
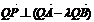 ;
;
(2)设直线AB的方程是 -2
-2 +12=0,过A、B两点的圆C与抛物线在点A处有共同的切线,求圆C的方程.
+12=0,过A、B两点的圆C与抛物线在点A处有共同的切线,求圆C的方程.
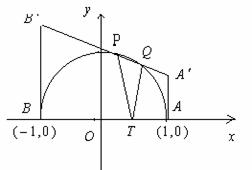
[例1]已知点T是半圆O的直径AB上一点,AB=2、OT=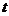 (0<
(0<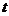 <1),以AB为直腰作直角梯形
<1),以AB为直腰作直角梯形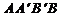 ,使
,使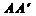 垂直且等于AT,使
垂直且等于AT,使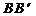 垂直且等于BT,
垂直且等于BT,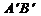 交半圆于P、Q两点,建立如图所示的直角坐标系.
交半圆于P、Q两点,建立如图所示的直角坐标系.
 (1)写出直线
(1)写出直线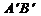 的方程;
的方程;
(2)计算出点P、Q的坐标;
(3)证明:由点P发出的光线,经AB反射后,反射光线通过点Q.
解: (1 ) 显然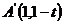 ,
, 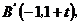 于是 直线
于是 直线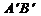 的方程为
的方程为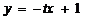 ;
;
(2)由方程组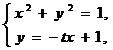 解出
解出 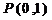 、
、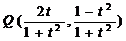 ;
;
(3)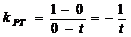 ,
, 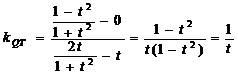 .
.
由直线PT的斜率和直线QT的斜率互为相反数知,由点P发出的光线经点T反射,反射光线通过点Q.
[例2]设P是圆M:( -5)2+(
-5)2+( -5)2=1上的动点,它关于A(9, 0)的对称点为Q,把P绕原点依逆时针方向旋转90°到点S,求|SQ|的最值.
-5)2=1上的动点,它关于A(9, 0)的对称点为Q,把P绕原点依逆时针方向旋转90°到点S,求|SQ|的最值.
解:设P( ,
, ),则Q(18-
),则Q(18- , -
, - ),记P点对应的复数为
),记P点对应的复数为 +
+
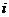 ,则S点对应的复数为: (
,则S点对应的复数为: ( +
+
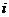 )·
)·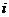 =-
=- +
+
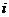 ,即S(-
,即S(- ,
,  )
)
∴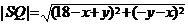
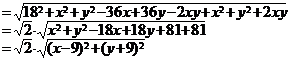
其中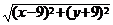 可以看作是点P到定点B(9,
-9)的距离,共最大值为
可以看作是点P到定点B(9,
-9)的距离,共最大值为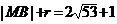 最小值为
最小值为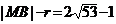 ,则
,则
|SQ|的最大值为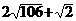 ,|SQ|的最小值为
,|SQ|的最小值为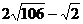 .
.
[例4](02年天津卷)已知两点M(-1,0),N(1,0)且点P使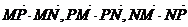 成公差小于零的等差数列,
成公差小于零的等差数列,
(1)点P的轨迹是什么曲线?
(2)若点P坐标为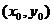 ,
,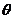 为
为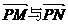 的夹角,求tanθ.
的夹角,求tanθ.
解:(1)记P( ,
,  ),由M(-1,0)N(1,0)得
),由M(-1,0)N(1,0)得
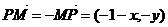
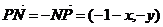
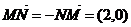
所以 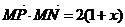
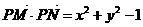
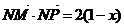
于是, 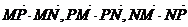 是公差小于零的等差数列等价于
是公差小于零的等差数列等价于
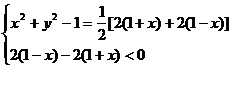 即
即 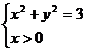
所以,点P的轨迹是以原点为圆心,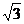 为半径的右半圆.
为半径的右半圆.
(2)点P的坐标为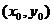 。
。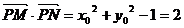 .
.
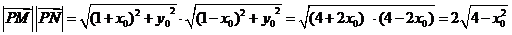
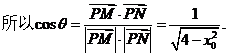 因为 0〈
因为 0〈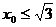 , 所以
, 所以
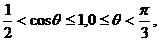
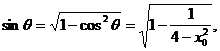
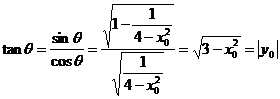 .
.
[例4]舰A在舰B的正东6千米处,舰C在舰B的北偏西30°且与B相距4千米,它们准备捕海洋动物,某时刻A发现动物信号,4秒后B、C同时发现这种信号,A发射麻醉炮弹.设舰与动物均为静止的,动物信号的传播速度为1千米/秒,炮弹的速度是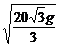 千米/秒,其中g为重力加速度,若不计空气阻力与舰高,问舰A发射炮弹的方位角和仰角应是多少?
千米/秒,其中g为重力加速度,若不计空气阻力与舰高,问舰A发射炮弹的方位角和仰角应是多少?
分析:答好本题,除要准确地把握好点P的位置(既在线段BC的垂直平分线上,又在以A、B为焦点的抛物线上),还应对方位角的概念掌握清楚.
技巧与方法:通过建立恰当的直角坐标系,将实际问题转化成解析几何问题来求解.对空间物体的定位,一般可利用声音传播的时间差来建立方程.
解:取AB所在直线为 轴,以AB的中点为原点,建立如图所示的直角坐标系.由题意可知,A、B、C舰的坐标为(3,0)、(-3,0)、(-5,2
轴,以AB的中点为原点,建立如图所示的直角坐标系.由题意可知,A、B、C舰的坐标为(3,0)、(-3,0)、(-5,2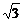 ).
).
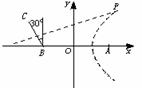
由于B、C同时发现动物信号,记动物所在位置为P,则|PB|=|PC|.于是P在线段BC的中垂线上,易求得其方程为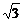
 -3
-3 +7
+7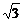 =0.
=0.
又由A、B两舰发现动物信号的时间差为4秒,知|PB|-|PA|=4,故知P在双曲线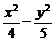 =1的右支上.
=1的右支上.
直线与双曲线的交点为(8,5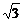 ),此即为动物P的位置,利用两点间距离公式,可得|PA|=10.
),此即为动物P的位置,利用两点间距离公式,可得|PA|=10.
据已知两点的斜率公式,得kPA=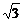 ,所以直线PA的倾斜角为60°,于是舰A发射炮弹的方位角应是北偏东30°.
,所以直线PA的倾斜角为60°,于是舰A发射炮弹的方位角应是北偏东30°.
设发射炮弹的仰角是θ,初速度v0=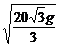 ,则
,则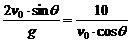 ,
,
∴sin2θ=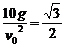 ,∴仰角θ=30°.
,∴仰角θ=30°.
答:方位角北偏东300,仰角30°.
解决圆锥曲线综合题,关键是熟练掌握每一种圆锥曲线的定义、标准方程、图形与几何性质,注意挖掘知识的内在联系及其规律,通过对知识的重新组合,以达到巩固知识、提高能力的目的.
(1)对于求曲线方程中参数的取值范围问题,需构造参数满足的不等式,通过求不等式(组)求得参数的取值范围;或建立关于参数的目标函数,转化为函数的值域.
(2)对于圆锥曲线的最值问题,解法常有两种:当题目的条件和结论能明显体现几何特征及意义,可考虑利用数形结合法解;当题目的条件和结论能体现一种明确的函数关系,则可先建立目标函数,再求这个函数的最值.
[例5]已知抛物线C: 2=4
2=4 .
.
(1)若椭圆左焦点及相应的准线与抛物线C的焦点F及准线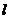 分别重合,试求椭圆短轴端点B与焦点F连线中点P的轨迹方程;
分别重合,试求椭圆短轴端点B与焦点F连线中点P的轨迹方程;
(2)若M(m,0)是 轴上的一定点,Q是(1)所求轨迹上任一点,试问|MQ|有无最小值?若有,求出其值;若没有,说明理由.
轴上的一定点,Q是(1)所求轨迹上任一点,试问|MQ|有无最小值?若有,求出其值;若没有,说明理由.
解:由抛物线 2=4
2=4 ,得焦点F(1,0),准线
,得焦点F(1,0),准线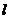 :
: =-1.
=-1.
(1)设P( ,
, ),则B(2
),则B(2 -1,2
-1,2 ),椭圆中心O′,则|FO′|∶|BF|=
),椭圆中心O′,则|FO′|∶|BF|=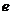 ,又设点B到
,又设点B到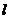 的距离为
的距离为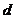 ,则|BF|∶
,则|BF|∶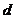 =
=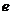 ,∴|FO′|∶|BF|=|BF|∶
,∴|FO′|∶|BF|=|BF|∶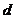 ,即(2
,即(2 -2)2+(2
-2)2+(2 )2=2
)2=2 (2
(2 -2),化简得P点轨迹方程为
-2),化简得P点轨迹方程为 2=
2= -1(
-1( >1).
>1).
(2)设Q( ,y),则
,y),则
|MQ|=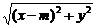
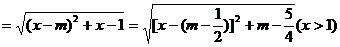
(ⅰ)当m-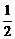 ≤1,即m≤
≤1,即m≤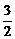 时,函数
时,函数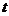 =[
=[ -(m-
-(m-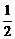 )2]+m-
)2]+m-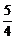 在(1,+∞)上递增,故
在(1,+∞)上递增,故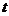 无最小值,亦即|MQ|无最小值.
无最小值,亦即|MQ|无最小值.
(ⅱ)当m-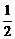 >1,即m>
>1,即m>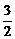 时,函数
时,函数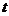 =[
=[ 2-(m-
2-(m-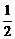 )2]+m-
)2]+m-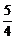 在
在 =m-
=m-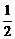 处有最小值m-
处有最小值m-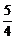 ,∴|MQ|min=
,∴|MQ|min=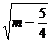 .
.
[例6]已知抛物线C的对称轴与 轴平行,顶点到原点的距离为5.若将抛物线C向上平移3个单位,则在
轴平行,顶点到原点的距离为5.若将抛物线C向上平移3个单位,则在 轴上截得的线段长为原抛物线C在
轴上截得的线段长为原抛物线C在 轴上截得的线段长的一半;若将抛物线C向左平移1个单位,则所得抛物线过原点,求抛物线C的方程.
轴上截得的线段长的一半;若将抛物线C向左平移1个单位,则所得抛物线过原点,求抛物线C的方程.
解:设所求抛物线方程为( -
-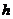 )2=
)2=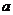 (
( -
-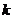 )(
)( 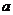 ∈R,
∈R, 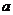 ≠0) ①
≠0) ①
由①的顶点到原点的距离为5,得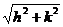 =5 ②
=5 ②
在①中,令 =0,得
=0,得 2-2
2-2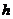
 +
+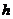 2+
2+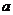
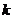 =0。设方程的二根为
=0。设方程的二根为 1,
1, 2,则
2,则
| 1-
1- 2|=2
2|=2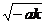 .
.
将抛物线①向上平移3个单位,得抛物线的方程为
( -h)2=
-h)2=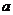 (
( -
-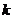 -3)
-3)
令 =0,得
=0,得 2-2
2-2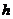
 +
+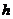 2+
2+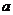
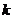 +3
+3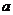 =0。设方程的二根为
=0。设方程的二根为 3,
3, 4,则
4,则
| 3-
3- 4|=2
4|=2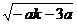 .
.
依题意得2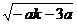 =
=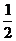 ·2
·2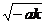 ,
,
即 4(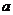
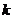 +3
+3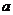 )=
)=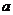
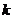 ③
③
将抛物线①向左平移1个单位,得( -
-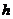 +1)2=
+1)2=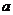 (
( -
-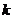 ),
),
由抛物线过原点,得(1-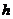 )2=-
)2=-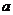
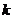 ④
④
由②③④得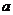 =1,
=1,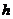 =3,
=3, 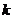 =-4或
=-4或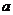 =4,
=4,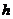 =-3,
=-3, 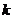 =-4.
=-4.
∴所求抛物线方程为( -3)2=
-3)2= +4,或(
+4,或( +3)2=4(
+3)2=4( +4).
+4).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com