22、已知=(x,0)，=(1，y)

(1)求点P(x，y)的轨迹C的方程；

(2)若直线：y=kx+m(km≠0)与曲线C交于A、B两端，D(0，-1),且有|AD|=|BD|，试求m的取值范围。

21、已知函数f(x)=a₀+a_1=x+a2_x²+a₃x³+…+a_nxⁿ(n∈Nⁿ)，且y=f(x)的图象经过点(1，n²)，数列{a_n}(n∈N⁺)为等差数列。

(1)求数列{a_n}的通项公式；

(2)当n为奇函数时，设g(x)=,是否存在自然数m和M，使不等式m<g()<M恒成立，若存在，求出M-m的最小值；若不存在，说明理由。

20、某银行准备新设一种定期存款业务，经预测，存款量与利率的平方成正比，比例系数为K(K>0)，货款的利率为4.8%，又银行吸收的存款能全部放货出去。

(1)若存款的利率为x，x∈(0，0.048)，试写出存款量g(x)及银行应支付给储户的利息(x)；

(2)存款利率定为多少时，银行可获得最大收益？

19、如图，直三棱柱ABC-A₁B₁C₁中，AB=AC=4,∠BAC=90°，侧面ABB₁A₁为正方形，D为正方形ABB₁A₁的中心，E为BC的中点。

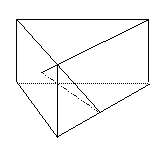(1)求证：平面DB₁E⊥平面BCC₁B₁；

(2)求异面直线A₁B与B₁E所成的角。

18、已知：A、B是△ABC的两个内角，，其中、为互相垂地的单位向量。若||=，试求tanA·tanB的值。

17、同时抛掷15枚均匀的硬币一次

(1)试求至多有1枚正面向上的概率；

(2)试问出现正面向上为奇函数的概率与出现正面向上为偶函数枚的概率是否相等？请说明理由。

16、下列四个命题

①函数f(x)=x+的值域是(-∞，-2]∪[2，+∞)；

②已知命题p与命题q，若p是q的充分不必要条件，则是的充分不必要条件；

③二项式(a+b)⁴的展开式中系数最大的项为第3项；

④方程|x|+|y|=1的曲线围成的图形的面积是4。其中正确命题的序号是　　　　 (把你认为正确的序号都填上)

15、已知x、y满足约束条件，则z=2x+y的最大值是　　　　 。

14、甲、乙两名射击运动员参加某大型运动会的预选赛，他们分别射击了5次，成绩如下表(单位：环)

如果甲、乙两人中只有1人入选，则入选的应是　　　　 。

13、函数f(x)=x²-tx+2在[1，2]上有反函数，则t的一切可取值的范围是　　　　 。