2．理解欧姆定律，并能解决有关电路的问题。

1．让学生明确电阻的定义式及电阻的单位，理解导体的U-I图像。

21.(本小题满分13分)

已知函数.

(Ⅰ)若函数f(x)有三个零点，且，，求函数f(x)的单调区间；

(Ⅱ)若，，求证：导函数在区间(0，2)内至少有一个零点；

(Ⅲ)在(Ⅱ)的条件下，若导函数的两个零点之间的距离不小于，求的取值范围.

[解析](I)因为，又，则

.　　　　　　　　　　　　　　　　　　　　　　　　　 (1分)

因为x₂，x₃是方程的两根，则

，.即.　　　　　　 　　　　　　　　　　　　　　　(2分)

又，即，所以，即，从而.

所以.　　　　　　　　　　　　　　　　　　　　　 　　　　(3分)

因为，由，得.

故的单调递减区间是，单调递增区间是.　　　　　　　　　 (4分)

(Ⅱ)因为，，所以，即.

因为，所以，即.　　　　　　　　　　　　　 (5分)

于是，，.　 (6分)

(1)当时，因为，则在区间内至少有一个零点.

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (7分)

(2)当时，因为，则在区间(1，2)内至少有一零点.

故导函数在区间(0，2)内至少有一个零点.　　　　　　　　　　　　　　　　　 (8分)

(Ⅲ)设m，n是导函数的两个零点，则，.

所以.　　　　　 (10分)

由已知，，则，即.

所以，即或.　　　　　　　　　　　　　　　　 (11分)

又，，所以，即.

因为，所以.　　　　　　　　　　　　　　 　　　　　　　　　　(12分)

综上分析，的取值范围是.　　　　　　　　　　　　　　　　　　　　　 (13分)

20.(本小题满分13分)

设双曲线，点A、B分别为双曲线C实轴的左端点和虚轴的上端点，点、分别为双曲线C的左、右焦点，点M、N是双曲线C的右支上不同两点，点Q为线段MN的中点．已知在双曲线C上存在一点P，使得．

(Ⅰ)求双曲线C的离心率；

(Ⅱ)设为正常数，若点Q在直线上，求直线MN在y轴上的截距的取值范围.

[解](Ⅰ)由题设，点，，，，其中.(1分)

因为，则.

设点P，则，所以，.　　　 (3分)

因为点P在双曲线上，所以，即.　　　 (4分)

因为，所以，即，故离心率．　　　　　　　　　　 (6分)

(Ⅱ)由(Ⅰ)知，则.　　　　　　　　　　　　　　　　 (7分)

若轴，则Q在x轴上，不合题意.

设直线MN的方程为，代入，得，即

.　　　　　　　　　　　　　　 (*)　　　　　　 (9分)

若，则MN与双曲线C的渐近线平行，不合题意.

设点，，，则

，，.　　　　　　　　　 (10分)

若点Q在直线上，则.

因为点M、N在双曲线的右支上，所以m≠0，从而k＝4.　　　 　　　　　　　　　　(11分)

此时，方程(*)可化为.

由，得.　　　　　　　　　　　　　　　　 (12分)

又M、N在双曲线C 的右支上，则，所以.

故直线MN在y轴上的截距的取值范围是．　　　　　　　　　　　　 (13分)

19.(本小题满分13分)

某创业投资公司计划在2010年向某企业投入800万元用于开发新产品，并在今后若干年内，每年的投入资金都比上一年减少.估计2010年可获得投资回报收入400万元，由于该项投资前景广阔，预计今后的投资回报收入每年都会比上一年增加.

(Ⅰ)设第年(2010年为第一年)的投入资金为万元，投资回报收入为万元，求和的表达式；

(Ⅱ)从哪一年开始，该投资公司前几年的投资回报总收入将超过总投入？

[解](Ⅰ)据题意，每年投入的资金依次成首项为800万元，公比为的等比数列，每年的投资回报收入依次成首项为400万元，公比为的等比数列.　　　　　　　　　　　　 (2分)

所以，. 　　　　　　　　　　　　　　　　　　　　(4分)

(Ⅱ)设经过年的总投入为S_n万元，总收入为T_n万元，则

，.　　　　　 (6分)

由，得，即.　 (7分)

设，代入上式整理得，，解得或(舍去).　　　 (9分)

当时，；当时，＝.　　　　　 　　　　　(11分)

因为是减函数，所以当时，有成立，从而成立.　 (12分)

答：从2014年开始，该投资公司前几年的投资回报总收入将超过总投入.　　　　　　 (13分)

18.(本小题满分12分)

在等腰直角三角形ABC中，D是斜边BC的中点，沿AD将△ABD折起，使∠BDC＝90°.

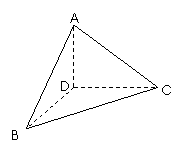
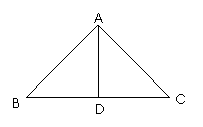(Ⅰ)求证：CD⊥平面ABD；

(Ⅱ)求二面角A-BC-D的余弦值.

[解](Ⅰ)因为△ABC是等腰直角三角形，D是斜边BC的中点，所以AD⊥CD. 　　(2分)

又∠BDC＝90°，所以BD⊥CD. 因为AD与BD交于点D，所以CD⊥面ABD.　　　 (5分)

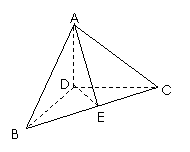(Ⅱ) 如图，取BC的中点E，连DE、AE

因为AB＝AC，则AE⊥BC. 因为BD＝CD，则DE⊥BC.

所以∠AED为二面角A-BC-D的平面角.　　　　　　　　　　　　　　　　　　　 (7分)

因为AD⊥BD，AD⊥CD，所以AD⊥面BCD.

设AD＝1，则BD＝DC＝1，AB＝AC＝BC＝.

从而△ABC是正三角形，所以AE＝.　　　　　　　　　　　　　　 (10分)

在Rt△ADE中，sin∠AED＝.　　　　　　　　　　　　　　　　　　　 (11分)

所以cos∠AED＝，故二面角A-BC-D的余弦值为.　　　　　　　　　　 (12分)

17.(本小题满分12分)

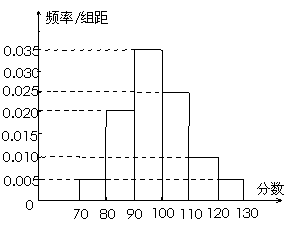某中学高三文科共有四个班，第二次月考后，随机在各班抽取了部分学生的数学成绩进行统计分析.已知各班被抽取的学生人数恰好成等差数列，且人数最少的班被抽取了22人. 从四个班抽取出来的所有学生的数学成绩的频率分布直方图如图所示，其中共有5人的成绩在120-130分(含120分但不含130分).

　　 (Ⅰ)求各班被抽取的学生人数各为多少人？

(Ⅱ)在被抽取的所有学生中任选一人，

求该生的数学成绩不小于90分的概率.

[解](Ⅰ)由频率分布直方图知，

成绩在120-130分的频率是0.005×10＝0.05.　　　　　　　　　　　　　　　　　 (2分)

又成绩在该分数段的人数为5，所以抽取的学生

总人数为人.　　　　　　　　　　　　　　　 　　　　　　　　　　　　(4分)

因为各班被抽取的学生人数成等差数列，

且首项为22，设其公差为，则

＝100，所以.

故各班被抽取的学生人数分别是22人，24人，26人，28人.　　　　　　　　　　　　 (8分)

(Ⅱ)由直方图知，分数不小于90分的频率为(0.035+0.025+0.01+0.005)×10＝0.75.

故在被抽取的所有学生中任选一人，该生的数学成绩不小于90分的概率是0.75.　　　 (12分)

16.(本小题满分12分)

如图，设A是单位圆和x轴正半轴的交点，P，Q是单位圆上两点，是坐标原点，且

，.

(Ⅰ)若点Q的坐标是，求的值；

(Ⅱ)设函数，求的值域．

[解](Ⅰ)由已知可得.　　　　　　　　　　　　　　　　　 (2分)

所以.　　　　　 (6分)

(Ⅱ).

(9分)

因为，则，所以.

故的值域是.　　　　　　　　　　　　　　　　　　　　　　　　　 (12分)

15.已知集合M＝{1，2，3，4}，，集合A中所有元素的乘积称为集合A的“累积值”，且规定：当集合A只有一个元素时，其累积值即为该元素的数值，空集的累积值为0. 设集合A的累积值为n.

(1)若n＝3，则这样的集合A共有 2 个；(2)若n为偶数，则这样的集合A共有 13 个.

[解析]若n＝3，据“累积值”的定义，得A＝{3}或A＝{1，3}，这样的集合A共有2个.

因为集合M的子集共有2⁴＝16个，其中“累积值”为奇数的子集为{1}，{3}，{1，3}共3个，所以“累积值”为偶数的集合共有13个.

14.设a＞0为常数，若对任意正实数x，y不等式恒成立，则的最小值为

　 4　 .

[解析]，当时取等号.

所以的最小值为，于是，所以a≥4，故的最小值为4.