
5.解:(1)由图象可知A=1,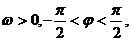 有
有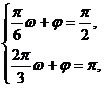
解之得: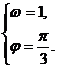
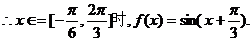
由 对称,可求得当
对称,可求得当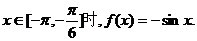
综上,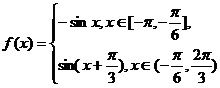
(2)因为 上有:
上有: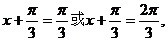
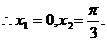 又
又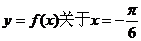 对称,
对称,
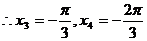 也是方程的解.
也是方程的解.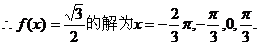
5.已知定义在区间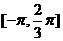 上的函数
上的函数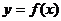 的图象关于直线
的图象关于直线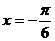 对称,当
对称,当
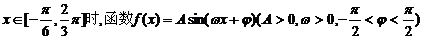 的图象如图.
的图象如图.
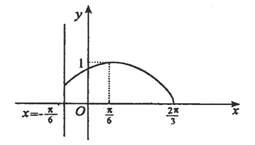 (1)求函数
(1)求函数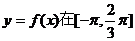 上的表达式;
上的表达式;
(2)求方程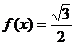 的解.
的解.
4、解: (Ⅰ)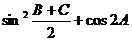 =
=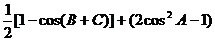
=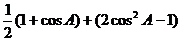 =
=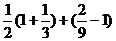 =
= 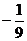
(Ⅱ) ∵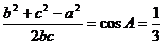 ,∴
,∴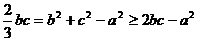 ,
,
又∵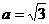 ∴
∴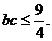 当且仅当 b=c=
当且仅当 b=c=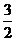 时,bc=
时,bc=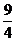 ,故bc的最大值是
,故bc的最大值是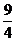 .
.
4、在△ABC中,角A、B、C所对的边分别为a,b,c,且cosA=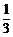 (Ⅰ)求sin2
(Ⅰ)求sin2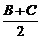 +cos2A的值;(Ⅱ)若a=
+cos2A的值;(Ⅱ)若a=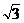 ,求bc的最大值。
,求bc的最大值。
3.解:(Ⅰ)由图象可知,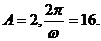
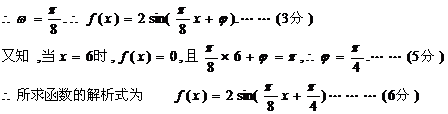
(Ⅱ)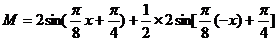
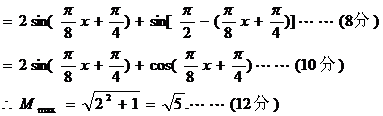
3、(本小题满分10分)已知函数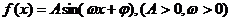 的图象如图所示.
的图象如图所示.
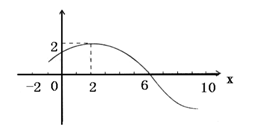 (Ⅰ)求函数f (x)的解析式;
(Ⅰ)求函数f (x)的解析式;
(Ⅱ)令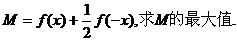
2、解: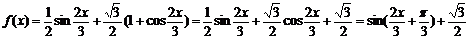
由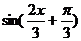 =0即
=0即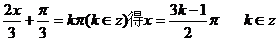
即对称中心的横坐标为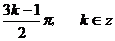
(Ⅱ)由已知b2=ac,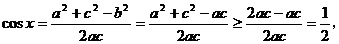
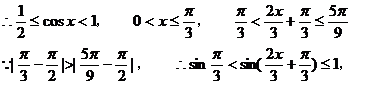
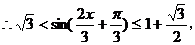 即
即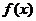 的值域为
的值域为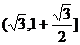 .
.
综上所述,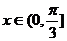 ,
, 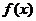 值域为
值域为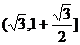 .
.
2、已知函数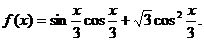 (Ⅰ)将f(x)写成
(Ⅰ)将f(x)写成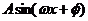 的形式,并求其图像对称中心的横坐标;(Ⅱ)如果△ABC的三边a、b、c满足b2=ac,且边b所对的角为x,试求x的范围及此时函数f(x)的值域.
的形式,并求其图像对称中心的横坐标;(Ⅱ)如果△ABC的三边a、b、c满足b2=ac,且边b所对的角为x,试求x的范围及此时函数f(x)的值域.
1、解:(I)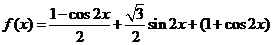
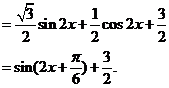
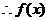 的最小正周期
的最小正周期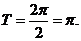
由题意得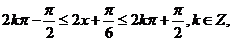 即
即 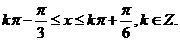
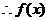 的单调增区间为
的单调增区间为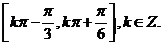
(II)方法一:先把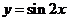 图象上所有点向左平移
图象上所有点向左平移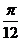 个单位长度,得到
个单位长度,得到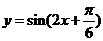 的图象,再把所得图象上所有的点向上平移
的图象,再把所得图象上所有的点向上平移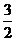 个单位长度,就得到
个单位长度,就得到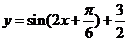 的图象
的图象
方法二:把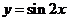 图象上所有的点按向量
图象上所有的点按向量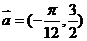 平移,就得到
平移,就得到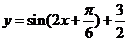 的图象
的图象
1、已知函数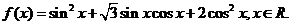
(I)求函数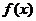 的最小正周期和单调增区间;
的最小正周期和单调增区间;
(II)函数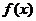 的图象可以由函数
的图象可以由函数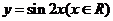 的图象经过怎样的变换得到?
的图象经过怎样的变换得到?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com