
2.


 若一次函数
若一次函数 的图象经过二、三、四象限,则二次函数
的图象经过二、三、四象限,则二次函数 的图象只可能是( )
的图象只可能是( )
A  B
B
 C
D
C
D
1.抛物线y=x2+2x-2的顶点坐标是 ( )
( )
A.(2,-2)  B.(1,-2) C.(1,-3) D.(-1,-3)
B.(1,-2) C.(1,-3) D.(-1,-3)
6.已知函数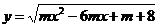 的定义域为R,且记
的定义域为R,且记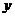 的最小值为
的最小值为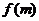 ,则当m变化时,函
,则当m变化时,函 数
数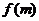 的值域为__________________
的值域为__________________
5.已知函数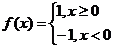 ,则不等式
,则不等式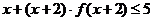 的解集是_____________
的解集是_____________
4.设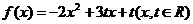 的最大值是
的最大值是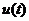 ,当
,当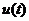 有最小值时,t的值为( )
有最小值时,t的值为( )
A.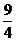 B.
B.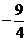 C.
C.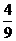 D.
D.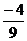
3.如果函数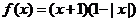 的图像在
的图像在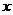 轴上方,则
轴上方,则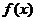 的定义域为( )
的定义域为( )
A.{x||x|<1} B. {x||x|>1} C. {x|x<1且x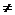 -1} D. {x|x>-1且x
-1} D. {x|x>-1且x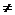 1}
1}
2.若函数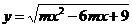 的定义域为R,则m的取值范围是(
的定义域为R,则m的取值范围是(  )
)
A.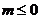 或
或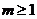 B.
B.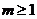 C.
C.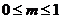 D.
D.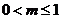
1.如果函数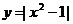 的图像与直线
的图像与直线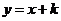 的交点恰为3个,则k的值为( )
的交点恰为3个,则k的值为( )
A.1
B.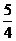 C.1或
C.1或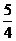 D.0或1
D.0或1
4、基本知识填空:
(1)、函数_____________________叫二 次函数,它的定义域是_________________
次函数,它的定义域是_________________ .
.
(2)、若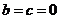 时,二次函数
时,二次函数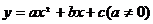
 是一条____________的抛物线,
是一条____________的抛物线,
(3)、二次函数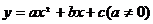 的顶点坐标为_______________,对称轴为_______;当
的顶点坐标为_______________,对称轴为_______;当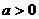 时,抛物线的开口_____________,在________________上是增函数,在_______
时,抛物线的开口_____________,在________________上是增函数,在_______ _____
_____
上是减函数;当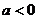 时,抛物线的开口__________
时,抛物线的开口__________ ___,在_________
___,在_________ _______上是增函数,在____________
_______上是增函数,在____________
上是减函数.
[例题解析]
例1、已知关于x的不 等式k
等式k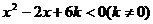
(1)若不等式的解集为{x|x<-3或x>-2},求k的值; [来源:]
[来源:]
(2)若不等式的解集为R,求k的值;
(3)若不等式的解集为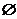 ,求k的值;
,求k的值;
(4)若不等式的解集为{x|2<x<3},求k的值;
例1、解析:(1)由题设知: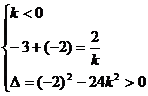
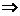 k=
k=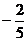
(2)由题设知: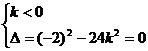
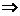 k
k =
=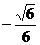
(3)由题设知: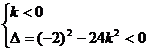
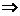 k<
k<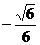
(3)由题设知: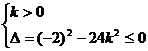
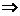 k
k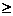
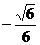 [来源:]
[来源:]
例2、已知f(x)=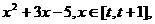 若f(x)的最小值为h(x),写出h(t)的表达式。
若f(x)的最小值为h(x),写出h(t)的表达式。
例2、解: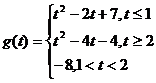
[课堂检测]
3、分析二次函数的性质时,需要对其解析式进项变形,主要用什么方法?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com