
22、(14分)已知定义域在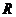 上的函数
上的函数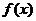 满足
满足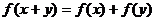 ,且当
,且当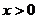 时,
时,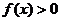 ,
,
(1)求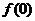 .
.
(2)判断函数的奇偶性,并证明之.
(3)解不等式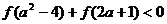 .
.
21、(12分)已知函数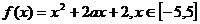 .
.
(1)求实数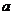 的范围,使
的范围,使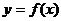 在区间
在区间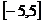 上是单调函数。
上是单调函数。
(2)求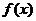 的最小值。
的最小值。
20、(12分)已知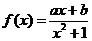 是定义在(-∞,+∞)上的函数,且满足
是定义在(-∞,+∞)上的函数,且满足
(1)求实数a,b,并确定函数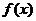 的解析式
的解析式
(2)用定义证明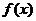 在(-1,1)上是增函数;
在(-1,1)上是增函数;
19、(12分)设函数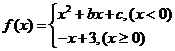 ,若
,若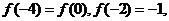
(1)求函数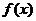 的解析式;
的解析式;
(2)画出函数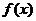 的图象,并说出函数
的图象,并说出函数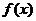 的单调区间;
的单调区间;
(3)若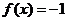 ,求相应
,求相应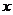 的值。
的值。
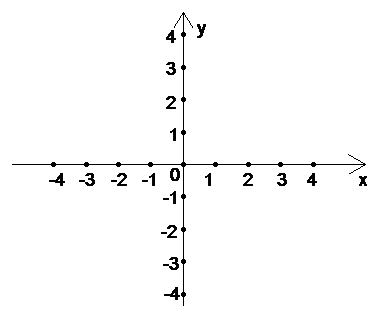
18、(12分)已知A=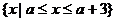 ,B=
,B=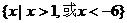 .
.
(1)若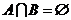 ,求
,求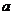 的取值范围;
的取值范围;
(2)若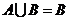 ,求
,求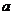 的取值范围.
的取值范围.
17、(12分)设全集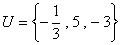 ,集合
,集合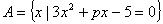 与集合
与集合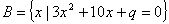 ,且
,且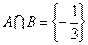 ,求
,求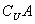 ,
,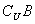
16、给出下列说法:①幂函数的图象一定不过第四象限;②奇函数图象一定过坐标原点;③ 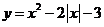 的递增区间为
的递增区间为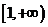 ;④定义在R上的函数
;④定义在R上的函数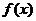 对任意两个不等实数a、b,总有
对任意两个不等实数a、b,总有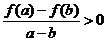 成立,则
成立,则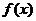 在R上是增函数;⑤
在R上是增函数;⑤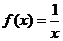 的单调减区间是
的单调减区间是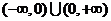 ;正确的有____________
;正确的有____________
15、函数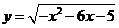 的值域为
的值域为
14、已知函数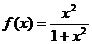 ,那么
,那么
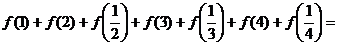 ____________
____________
13、 已知幂函数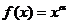 的图象经过点(9,3),则
的图象经过点(9,3),则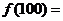
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com