3．例一、已知向量、，求作向量+

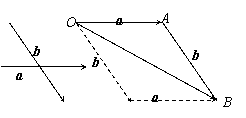
　 作法：在平面内取一点，作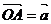 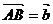，则.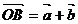

2、三角形法则(“首尾相接，首尾连”)

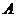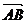如图，已知向量a、b.在平面内任取一点，作＝a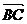，＝b，则向量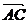叫做a与b的和，记作a+b，即 a+b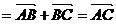，规定：　　　 a + 0-= 0 +

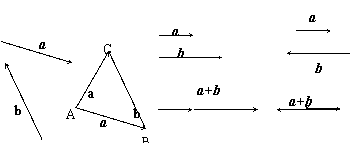
探究：(1)两相向量的和仍是一个向量；

(2)当向量与不共线时，+的方向不同向，且|+|<||+||；

(3)当与同向时，则+、、同向，且|+|=||+||，当与反向时，若||>||，则+的方向与相同，且|+|=||-||；若||<||，则+的方向与相同，且|+b|=||-||.

(4)“向量平移”(自由向量)：使前一个向量的终点为后一个向量的起点，可以推广到n个向量连加

1、向量的加法：求两个向量和的运算，叫做向量的加法.

2、　 情景设置：

(1)某人从A到B，再从B按原方向到C，

　 则两次的位移和：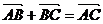

(2)若上题改为从A到B，再从B按反方向到C，

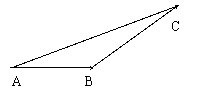　 则两次的位移和：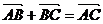

(3)某车从A到B，再从B改变方向到C，

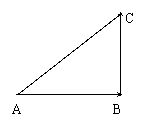　 则两次的位移和：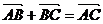

(4)船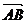速为，水速为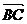，则两速度和：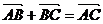

1、　　 复习：向量的定义以及有关概念

强调：向量是既有大小又有方向的量.长度相等、方向相同的向量相等.因此，我们研究的向量是与起点无关的自由向量，即任何向量可以在不改变它的方向和大小的前提下，移到任何位置

3、　 通过将向量运算与熟悉的数的运算进行类比，使学生掌握向量加法运算的交换律和结合律，并会用它们进行向量计算，渗透类比的数学方法；

教学重点：会用向量加法的三角形法则和平行四边形法则作两个向量的和向量.

教学难点：理解向量加法的定义.

学　 法：

数能进行运算，向量是否也能进行运算呢？数的加法启发我们，从运算的角度看，位移的合成、力的合成可看作向量的加法.借助于物理中位移的合成、力的合成来理解向量的加法，让学生顺理成章接受向量的加法定义.结合图形掌握向量加法的三角形法则和平行四边形法则.联系数的运算律理解和掌握向量加法运算的交换律和结合律.

教　 具：多媒体或实物投影仪，尺规

授课类型：新授课

教学思路：

2、　 会用向量加法的三角形法则和平行四边形法则作两个向量的和向量，培养数形结合解决问题的能力；

　　 书本88页习题2.1第3、5题

(吴春霞)

第2课时

§2.2.1　 向量的加法运算及其几何意义

教学目标：

1、　 掌握向量的加法运算，并理解其几何意义；

3、 向量的图示，要标上箭头和始点、终点.

2、 平行向量不是平面几何中的平行线段的简单类比.